
分析 (1)設等比數列{an}的公比為q,由題意得$\frac{2}{3}$+$\frac{2}{3}$q+$\frac{1}{2}$•$\frac{2}{3}$q=1,解得q,即可得出.
(2)由(1)知:bn=log3$\frac{{{a}_{n}}^{2}}{4}$=log33-2n=-2n,$\frac{1}{{b}_{n}•{b}_{n+1}}$=$\frac{1}{2n•(2n+2)}$=$\frac{1}{4}(\frac{1}{n}-\frac{1}{n+1})$.利用裂項求和方法即可得出.
解答 解:(1)設等比數列{an}的公比為q,由題意得$\frac{2}{3}$+$\frac{2}{3}$q+$\frac{1}{2}$•$\frac{2}{3}$q=1,即q=$\frac{1}{3}$,
因此an=a1•qn-1=$\frac{2}{{3}^{n}}$.
(2)由(1)知:bn=log3$\frac{{{a}_{n}}^{2}}{4}$=log33-2n=-2n,
∴$\frac{1}{{b}_{n}•{b}_{n+1}}$=$\frac{1}{2n•(2n+2)}$=$\frac{1}{4}(\frac{1}{n}-\frac{1}{n+1})$.
∴數列{$\frac{1}{{b}_{n}•{b}_{n+1}}$}的前n項和Tn=$\frac{1}{4}$$[(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})$+…+$(\frac{1}{n}-\frac{1}{n+1})]$
=$\frac{1}{4}(1-\frac{1}{n+1})$=$\frac{n}{4n+4}$.
點評 本題考查了數列遞推關系、等比數列的通項公式、裂項求和方法、對數運算性質,考查了推理能力與計算能力,屬于中檔題.


 新課標同步訓練系列答案
新課標同步訓練系列答案 一線名師口算應用題天天練一本全系列答案
一線名師口算應用題天天練一本全系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\overrightarrow a⊥\overrightarrow e$ | B. | $\overrightarrow a⊥(\overrightarrow a-2\overrightarrow e)$ | C. | $\overrightarrow e⊥(\overrightarrow a-2\overrightarrow e)$ | D. | $(\overrightarrow a+2\overrightarrow e)⊥(\overrightarrow a-2\overrightarrow e)$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 5 | B. | -5 | C. | 10 | D. | -10 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
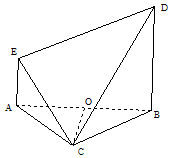 如圖,等邊△ABC與直角梯形ABDE所在平面垂直,BD∥AE,AE⊥AB,BC=BD=2AE=2,O為AB的中點.
如圖,等邊△ABC與直角梯形ABDE所在平面垂直,BD∥AE,AE⊥AB,BC=BD=2AE=2,O為AB的中點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{\sqrt{3}}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com