
分析 設f(x)=$\sqrt{-{x}^{2}+4x-3}$,如圖所示,表示以(2,0)為圓心,1為半徑的半圓,由圓心(2,0)到y=ax+a的距離$\frac{|3a|}{\sqrt{{a}^{2}+1}}$=1,可得a=$\frac{\sqrt{2}}{4}$,結合圖象可得結論.
解答  解:設f(x)=$\sqrt{-{x}^{2}+4x-3}$,如圖所示,表示以(2,0)為圓心,1為半徑的半圓,
解:設f(x)=$\sqrt{-{x}^{2}+4x-3}$,如圖所示,表示以(2,0)為圓心,1為半徑的半圓,
由圓心(2,0)到y=ax+a的距離$\frac{|3a|}{\sqrt{{a}^{2}+1}}$=1,
可得a=$\frac{\sqrt{2}}{4}$,
∵方程$\sqrt{-{x}^{2}+4x-3}$=ax+a有兩個不相等的實數根,
∴實數a的取值范圍為[0,$\frac{\sqrt{2}}{4}$).
故答案為[0,$\frac{\sqrt{2}}{4}$).
點評 本題考查方程根的研究,考查數形結合的數學思想,正確作出函數的圖象是關鍵.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:選擇題
| A. | -4 | B. | -3 | C. | 4 | D. | $2\sqrt{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -3 | B. | -5 | C. | -8 | D. | 8 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
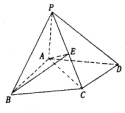 在四棱錐P-ABCD中,△ABC為正三角形,AB⊥AD,AC⊥CD,PA⊥平面ABCD,PC與平面ABCD所成角為45°
在四棱錐P-ABCD中,△ABC為正三角形,AB⊥AD,AC⊥CD,PA⊥平面ABCD,PC與平面ABCD所成角為45°查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
 秦九韶是我國南宋時期的數學家,普州(現四川省安岳縣)人,他在所著的《數書九章》中提出的多項式求值的秦九韶算法,至今仍是比較先進的算法,如圖所示的程序框圖給出了利用秦九韶算法求某多項式值的一個實例,若輸入x的值為2,則輸出v的值為( )
秦九韶是我國南宋時期的數學家,普州(現四川省安岳縣)人,他在所著的《數書九章》中提出的多項式求值的秦九韶算法,至今仍是比較先進的算法,如圖所示的程序框圖給出了利用秦九韶算法求某多項式值的一個實例,若輸入x的值為2,則輸出v的值為( )| A. | 210-1 | B. | 210 | C. | 310-1 | D. | 310 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,-2)∪(2,+∞) | B. | (-2,0)∪(0,2) | C. | {x|x≠±2} | D. | (-2,2) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com