
分析 (1)利用函數的導數f′(x)>0在(a,b)上恒成立,則f(x)在(a,b)上是增函數,f′(x)>0的解集與定義域的交集的對應區間為增區間;
若f′(x)<0在(a,b)上恒成立,則f(x)在(a,b)上是減函數,f′(x)<0的解集與定義域的交集的對應區間為減區間.
(2)利用可導函數在某點處的導數是該點處切線的斜率k,k=f'(x)=ex•ex,通過求函數f'(x)=ex•ex值域,從而求得斜率k的范圍,在由k=tanα,求得α的取值范圍.
(3)通過g'(x)=ex-6x,得到函數的單調性,求出函數的最值(極值)的正負,從而得到函數與X軸的交點個數,也就是零點個數.
解答 解:(1)當a>0時,f(x)的單調遞增區間為(0,+∞),f(x)的單調遞減區間為(-∞,0),
當a<0時,f(x)的單調遞增區間為(-∞,0),f(x)的單調遞減區間為(0,+∞);
(2)曲線y=f(x)上任意一點的切線的斜率k=f'(x)=ex•ex,令F(x)=ex•ex,則F'(x)=eex•(x+1),由F'(x)=0,得x=-1,列表如下:
| x | (-∞,-1) | (-1,+∞) |
| F'(x) | - | + |
| F(x) | ↓ | ↑ |
| x | (-∞,0) | (0,2) | (2,+∞) |
| h'(x) | + | - | + |
| h(x) | ↑ | ↓ | ↑ |
| x | (-∞,x1) | (x1,x2) | (x2,+∞) |
| g'(x) | + | - | + |
| g(x) | ↑ | ↓ | ↑ |
| x | (-∞,0) | (0,2) | (2,+∞) |
| h'(x) | + | - | + |
| h(x) | ↑ | ↓ | ↑ |
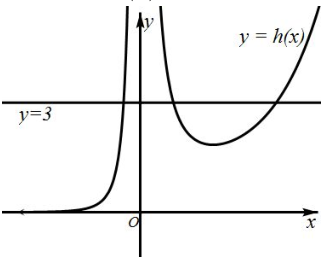
點評 本題第(1)問考查了函數的導數f′(x)的正負與函數單調性的關系,第(2)考查了導函數的幾何意義,第(3)問通過求出函數的最值(極值),通過函數草圖得到函數與X軸的交點個數,也就是零點個數,屬于中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| x(面積) | 4 | 6 | 9 | 7 | 8 | 8 |
| y(銷售額) | 3 | 5 | 6 | 4 | 5 | 7 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
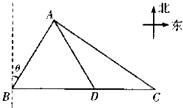 如圖,某流動海洋觀測船開始位于燈塔B的北偏東$θ(0<θ<\frac{π}{2})$方向,且滿足$2{sin^2}(\frac{π}{4}+θ)-\sqrt{3}$cos2θ=1,AB=AD,在接到上級命令后,該觀測船從A點位置沿AD方向在D點補充物資后沿BD方向在C點投放浮標,使得C點與A點的距離為4$\sqrt{3}$km,
如圖,某流動海洋觀測船開始位于燈塔B的北偏東$θ(0<θ<\frac{π}{2})$方向,且滿足$2{sin^2}(\frac{π}{4}+θ)-\sqrt{3}$cos2θ=1,AB=AD,在接到上級命令后,該觀測船從A點位置沿AD方向在D點補充物資后沿BD方向在C點投放浮標,使得C點與A點的距離為4$\sqrt{3}$km,查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 充分條件 | B. | 必要條件 | ||
| C. | 充要條件 | D. | 既不充分也不必要條件 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com