
分析 (Ⅰ)當n≥2,an=Sn-Sn-1,可得an+1+2=2(an+2),因此數列{an+2}是首項為4,公比為2的等比數列,即可求得數列{an}的通項公式;
(Ⅱ)由題意可得數列{bn}是等差數列,公差d=4,b1,b2,b5成等比數列,求得b1=2,求得bn=4n-2,$\frac{b_n}{{{a_n}+2}}=\frac{2n-1}{2^n}$,利用“錯位相減法”即可求得${T_n}=3-\frac{2n+3}{2^n}$.
解答 解:(Ⅰ)由Sn=an+1-2(n+1)(n∈N*)①
當n≥2,Sn-1=an-2n,②,
①-②得an=an+1-an-2,即an+1+2=2(an+2)(n≥2)…(3分)
又由①得a2=a1+4=6,
∴a2+2=2(a1+2)=8
∴數列{an+2}是首項為4,公比為2的等比數列…(5分)
∴${a_n}+2=4×{2^{n-1}}={2^{n+1}}$,
∴數列{an}的通項公式${a_n}={2^{n+1}}-2$;…(6分)
(Ⅱ)證明:由題設知數列{bn}是等差數列,公差d=4
又b1,b2,b5成等比數列,
∴${({b_1}+4)^2}={b_1}({b_1}+16)$,
解得b1=2,
∴bn=4n-2…(8分)
∴$\frac{b_n}{{{a_n}+2}}=\frac{2n-1}{2^n}$,
∴${T_n}=\frac{1}{2}+\frac{3}{2^2}+\frac{5}{2^3}+…+\frac{2n-1}{2^n}$,③
$\frac{1}{2}{T_n}=\frac{1}{2^2}+\frac{3}{2^3}+…+\frac{2n-3}{2^n}+\frac{2n-1}{{{2^{n+1}}}}$,④
③-④得,$\frac{1}{2}{T_n}=\frac{1}{2}+\frac{2}{2^2}+\frac{2}{2^3}+…+\frac{2}{2^n}-\frac{2n-1}{{{2^{n+1}}}}$,
∴${T_n}=1+1+\frac{1}{2}+\frac{1}{2^2}+…+\frac{1}{{{2^{n-2}}}}-\frac{2n-1}{2^n}$,
=$1+\frac{{1-\frac{1}{{{2^{n-1}}}}}}{{1-\frac{1}{2}}}-\frac{2n-1}{2^n}$,
=$3-\frac{2n+3}{2^n}$,
∴${T_n}=3-\frac{2n+3}{2^n}$.…(12分)
點評 本題考查等比數列通項公式,等比數列性質,考查“錯位相減法”求數列的前n項和,考查計算能力,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{7}$ | B. | -$\frac{1}{7}$ | C. | $\frac{4\sqrt{3}}{7}$ | D. | -$\frac{4\sqrt{3}}{7}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [1,3] | B. | (1,3) | C. | [-3,-1] | D. | (-3,-1) |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
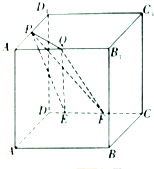 如圖,在棱長為a的正方體ABCD-A1B1C1D1中,P為A1D1的中點,Q為A1B1上任意一點,E,F為CD上任意兩點,且EF的長為定值,則以下四個值中為定值的編號是①②④.
如圖,在棱長為a的正方體ABCD-A1B1C1D1中,P為A1D1的中點,Q為A1B1上任意一點,E,F為CD上任意兩點,且EF的長為定值,則以下四個值中為定值的編號是①②④.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{63}{65}$ | B. | $\frac{33}{65}$ | C. | $\frac{16}{65}$ | D. | $-\frac{33}{65}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com