
| A. | 若數列{an}是公差為d的等差數列,則數列{$\frac{{S}_{n}}{n}$}的公差為$\fracp9vv5xb5{2}$的等差數列 | |
| B. | 若數列{$\frac{{S}_{n}}{n}$}是公差為d的等差數列,則數列{an}是公差為2d的等差數列 | |
| C. | 若數列{an}是等差數列,則數列的奇數項,偶數項分別構成等差數列 | |
| D. | 若數列{an}的奇數項,偶數項分別構成公差相等的等差數列,則{an}是等差數列 |
分析 根據等差數列的通項公式和前n項和公式進行分析,并作出判斷.
解答 解:A、若等差數列{an}的首項為a1,公差為d,前n項的和為Sn,則數列{$\frac{{S}_{n}}{n}$}為等差數列,且通項為$\frac{{S}_{n}}{n}$=a1+(n-1)$\fracp9vv5xb5{2}$,即數列{$\frac{{S}_{n}}{n}$}的公差為$\fracp9vv5xb5{2}$的等差數列,故說法正確;
B、由題意得:$\frac{{S}_{n}}{n}$=a1+(n-1)d,所以Sn=na1+n(n-1)d,則an=Sn-Sn-1=a1+2(n-1)d,即數列{an}是公差為2d的等差數列,故說法正確;
C、若數列{an}是等差數列的公差為d,則數列的奇數項,偶數項都是公差為2d的等差數列,說法正確;
D、若數列{an}的奇數項,偶數項分別構成公差相等的等差數列,則{an}不一定是等差數列,例如:{1,4,3,6,5,8,7},說法錯誤.
故選:D.
點評 本題考查等差數列的性質,考查等差數列的求和公式,考查運算與推理、證明的能力,屬于中檔題.


 活力課時同步練習冊系列答案
活力課時同步練習冊系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
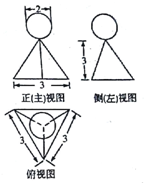 某幾何體的三視圖如圖所示,則該幾何體的體積為( )
某幾何體的三視圖如圖所示,則該幾何體的體積為( )| A. | $\frac{4π}{3}$+$\frac{9\sqrt{3}}{4}$ | B. | $\frac{4π}{3}$+$\frac{27\sqrt{3}}{4}$ | C. | $\frac{8π}{3}$+$\frac{9\sqrt{3}}{4}$ | D. | $\frac{8π}{3}$+$\frac{27\sqrt{3}}{4}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
 已知f(x)=Asin (ω x+φ)+(A>0,ω>0,|φ|<π})的圖象如圖所示,則f(3π)=( )
已知f(x)=Asin (ω x+φ)+(A>0,ω>0,|φ|<π})的圖象如圖所示,則f(3π)=( )| A. | -$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com