
 開心練習課課練與單元檢測系列答案
開心練習課課練與單元檢測系列答案 開心試卷期末沖刺100分系列答案
開心試卷期末沖刺100分系列答案科目:高中數學 來源: 題型:選擇題
| A. | g(x)可能沒有零點 | B. | g(x)可能有1個零點 | C. | g(x)可能有2個零點 | D. | g(x)可能有3個零點 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
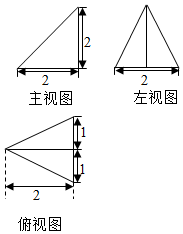 已知某個幾何體的三視圖如圖所示,根據圖中標出的尺寸,可得出這個幾何體的內切球半徑是( )
已知某個幾何體的三視圖如圖所示,根據圖中標出的尺寸,可得出這個幾何體的內切球半徑是( )| A. | $\frac{4}{3}$ | B. | $\frac{4}{9}$ | C. | $\sqrt{6}-2$ | D. | $3\sqrt{6}-6$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 若數列{an}是公差為d的等差數列,則數列{$\frac{{S}_{n}}{n}$}的公差為$\fracp9vv5xb5{2}$的等差數列 | |
| B. | 若數列{$\frac{{S}_{n}}{n}$}是公差為d的等差數列,則數列{an}是公差為2d的等差數列 | |
| C. | 若數列{an}是等差數列,則數列的奇數項,偶數項分別構成等差數列 | |
| D. | 若數列{an}的奇數項,偶數項分別構成公差相等的等差數列,則{an}是等差數列 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
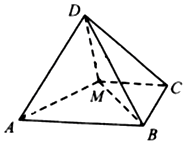 如圖,四棱錐D-ABCM中,AD⊥DM,底面四邊形ABCM是直角梯形,AB⊥BC,MC⊥BC,且AB=2BC=2CM=4,平面AMD⊥平面ABCM.
如圖,四棱錐D-ABCM中,AD⊥DM,底面四邊形ABCM是直角梯形,AB⊥BC,MC⊥BC,且AB=2BC=2CM=4,平面AMD⊥平面ABCM.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{8}$ | B. | $-\frac{1}{8}$ | C. | $-\frac{7}{8}$ | D. | $\frac{7}{8}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com