
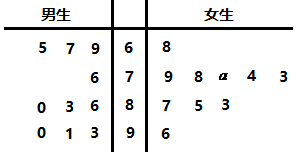
 某中學為了普及法律知識,舉行了一次法律知識競賽活動.下面的莖葉圖記錄了男生、女生各10名學生在該次競賽活動中的成績(單位:分).
某中學為了普及法律知識,舉行了一次法律知識競賽活動.下面的莖葉圖記錄了男生、女生各10名學生在該次競賽活動中的成績(單位:分).分析 (1)分別求出男生的平均成績和女生的平均成績,得到關于a的方程,解出即可;
(2)列出從成績高于86分的學生中任意抽取3名學生所有抽取的結果以及滿足條件的結果,從而求出滿足條件的概率即可.
解答 解:(1)男生的平均成績為$\overline{x}$=$\frac{1}{10}$(3×90+3×80+70+3×60+1+3+3+6+6+9+7+5)=80,
女生的平均成績為$\overline{y}$=$\frac{1}{10}$(90+3×80+5×70+60+6+7+5+3+9+8+a+4+3+8)=$\frac{793+a}{10}$,
由題意得:$\overline{x}$=$\overline{y}$,即$\frac{793+a}{10}$=80,解得:a=7;
(2)從成績高于86分的學生中任意抽取3名學生,
所有抽取的結果是(96,93,91),(96,93,90),(96,93,87),(96,91,90),
(96,91,87),(96,09,87),(93,91,90),(93,91,87),(93,90,87),(91,90,87)
共10種情況.
其中恰有2名學生是女生的結果是(96,93,87),(96,91,87),(96,90,87)共3種情況.
所以從成績高于8(6分)的學生中抽取了3名學生恰有2名是女生的概率P=$\frac{3}{10}$.
點評 本題考查了平均數的求法,考查條件概率問題,是一道基礎題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:選擇題
| A. | 最大值為-$\frac{1}{2}$ | B. | 最小值為-$\frac{1}{2}$ | C. | 最大值為1 | D. | 最小值為1 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [-1,+∞) | B. | (-∞,-1) | C. | (-∞,+∞) | D. | [-1,1)∪(1,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{7}{5}$ | B. | $\frac{5}{7}$ | C. | $±\frac{7}{12}$ | D. | $\frac{5}{12}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {-1,0,1} | B. | {0,1,2} | C. | {1,2,3} | D. | {1,2,3,4} |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ① | B. | ② | C. | ②④ | D. | ③ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com