
分析 解法一:(Ⅰ)要使f(x)≥0有唯一解,只需滿足f(x)max=0,且f(x)max=0的解唯一,分①當k≤0,②當k>0 討論求解;
(Ⅱ)要證當a≤1時,x(f(x)+kx-k)<ex-ax2-1,即證當a≤1時,ex-ax2-xlnx-1>0,即證ex-x2-xlnx-1>0.由(Ⅰ)得xlnx≤x(x-1),故只需證ex-2x2+x-1>0,當x>0時成立;
解法二:(Ⅰ)分①當k≤0時,②當k>0時兩種情況求解,
(Ⅱ)要證明當a≤1時,x(f(x)+kx-k)<ex-ax2-1,即證當a≤1時,ex-ax2-xlnx-1>0,(因為ax2≤x2),即證ex-x2-xlnx-1>0
解答 解法一:(Ⅰ)函數f(x)的定義域為(0,+∞).
要使f(x)≥0有唯一解,只需滿足f(x)max=0,且f(x)max=0的解唯一,(1分)$f'(x)=\frac{1-kx}{x}$,(2分)
①當k≤0時,f'(x)≥0,f(x)在(0,+∞)上單調遞增,且f(1)=0,
所以f(x)≥0的解集為[1,+∞),不符合題意; (4分)
②當k>0時,且$x∈(0,\frac{1}{k}]$時,f'(x)≥0,f(x)單調遞增;當$x∈(\frac{1}{k},+∞)$時,f'(x)<0,f(x)單調遞減,所以f(x)有唯一的一個最大值為$f(\frac{1}{k})$,
令$f(\frac{1}{k})=k-lnk-1=0$,得k=1,此時f(x)有唯一的一個最大值為f(1),且f(1)=0,故f(x)≥0的解集是{1},符合題意;
綜上,可得k=1.(6分)
(Ⅱ)要證當a≤1時,x(f(x)+kx-k)<ex-ax2-1,
即證當a≤1時,ex-ax2-xlnx-1>0,
即證ex-x2-xlnx-1>0.(7分)
由(Ⅰ)得,當k=1時,f(x)≤0,即lnx≤x-1,從而xlnx≤x(x-1),
故只需證ex-2x2+x-1>0,當x>0時成立; (8分)
令h(x)=ex-2x2+x-1(x≥0),則h'(x)=ex-4x+1,(9分)
令F(x)=h'(x),則F'(x)=ex-4,令F'(x)=0,得x=2ln2.
因為F'(x)單調遞增,所以當x∈(0,2ln2]時,F'(x)≤0,F(x)單調遞減,即h'(x)單調遞減,當x∈(2ln2,+∞)時,F'(x)>0,F(x)單調遞增,即h'(x)單調遞增,
所以h'(ln4)=5-8ln2<0,h'(0)=2>0,h'(2)=e2-8+1>0,
由零點存在定理,可知?x1∈(0,2ln2),?x2∈(2ln2,2),使得h'(x1)=h'(x2)=0,
故當0<x<x1或x>x2時,h'(x)>0,h(x)單調遞增;當x1<x<x2時,h'(x)<0,h(x)單調遞減,所以h(x)的最小值是h(0)=0或h(x2).
由h'(x2)=0,得${e^{x_2}}=4{x_2}-1$,h(x2)=${e^{x_2}}-2{x_2}^2+{x_2}-1=-2{x_2}^2+5{x_2}-2=-({{x_2}-2})({2{x_2}-1})$,
因為x2∈(2ln2,2),所以h(x2)>0,
故當x>0時,h(x)>0,所以原不等式成立.(12分)
解法二:(Ⅰ)函數f(x)的定義域為(0,+∞).$f'(x)=\frac{1-kx}{x}$,(1分)
①當k≤0時,f'(x)≥0,f(x)在(0,+∞)上單調遞增,且f(1)=0,所以f(x)≥0的解為[1,+∞),此時不符合題意; (2分)
②當k>0時,$f'(x)=\frac{1-kx}{x}=-\frac{k}{x}(x-\frac{1}{k})$,
所以當$x∈(0,\frac{1}{k}]$時,f'(x)≥0,f(x)單調遞增;當$x∈(\frac{1}{k},+∞)$時,f'(x)<0,f(x)單調遞減,所以$f(x)≤f(\frac{1}{k})$,$f(\frac{1}{k})=k-lnk-1$,(3分)
令g(k)=k-lnk-1,$g'(k)=1-\frac{1}{k}=\frac{k-1}{k}$,(4分)
當k∈(0,1]時,g'(k)≤0,g(k)單調遞減,當k∈(1,+∞)時,g'(k)>0,g(k)單調遞增,所以g(k)≥g(1)=0,由此可得當k>0且k≠1時,$f(\frac{1}{k})>0$,
且當x→0+,x→+∞時,f(x)→-∞,由零點存在定理,$?{x_1}∈(0,\frac{1}{k}),{x_2}∈(\frac{1}{k},+∞)$,
使得f(x1)=f(x2)=0,當x1≤x≤x2時,f(x)≥0,解集不唯一,不符合題意;
當k=1時,f(x)≤f(1)=0,所以f(x)≥0的解集是{1},符合題意;
綜上可得,當k=1時,f(x)≥0有唯一解; (6分)
(Ⅱ)要證明當a≤1時,x(f(x)+kx-k)<ex-ax2-1,
即證當a≤1時,ex-ax2-xlnx-1>0,(因為ax2≤x2)
即證ex-x2-xlnx-1>0,(7分)
令F(x)=ex-x2-xlnx-1(x>0),則F'(x)=ex-2x-lnx-1,(8分)
令G(x)=F'(x),則$G'(x)={e^x}-2-\frac{1}{x}$在(0,+∞)上單調遞增,且G'(1)<0,G'(2)>0,
所以?x0∈(1,2)使得G'(x0)=0,即${e^{x_0}}=2+\frac{1}{x_0}$,
所以當x>x0時,G'(x)>0,G(x)單調遞增,即F'(x)遞增;
當0<x<x0時,G'(x)<0,G(x)單調遞減,即F'(x)遞減,
所以$F'{({x_0})_{min}}={e^{x_0}}-2{x_0}-ln{x_0}-1=\frac{1}{x_0}-2{x_0}-ln{x_0}+1$,$H(x)=\frac{1}{x}-2x-lnx+1$,
當x∈(1,2)時遞減,F'(x0)min<H(1)=0,
當x→0時,F'(x)→+∞,$F'(\frac{3}{2})={e^{\frac{3}{2}}}-3-ln\frac{3}{2}-1>0$,
由零點存在定理,可得?x1∈(0,x0),${x_2}∈({x_0},\frac{3}{2})$,F'(x1)=F'(x2)=0,
故當0<x<x1或x>x2時,F'(x)>0,F(x)單調遞增,
當x1<x<x2時,F'(x)<0,F(x)單調遞減,
當x→0+時,F(x)→0,由F'(x2)=0得,${e^{x_2}}=2{x_2}+ln{x_2}+1$,$1<{x_0}<{x_2}<\frac{3}{2}$,
又F(x2)=${e^{x_2}}-{x_2}^2-{x_2}ln{x_2}-1=-{x_2}^2+2{x_2}+ln{x_2}-{x_2}ln{x_2}$,
令M(x)=-x2+2x+lnx-xlnx($1<x<\frac{3}{2}$),
則$M'(x)=-2x+2+\frac{1}{x}-lnx-1$在$(1,\frac{3}{2})$遞減,且M'(1)=0,所以M'(x)<0,
所以M(x)在$(1,\frac{3}{2})$遞減,$M(\frac{3}{2})=-\frac{9}{4}+3+ln\frac{3}{2}-\frac{3}{2}ln\frac{3}{2}=0.75-\frac{1}{2}(ln3-ln2)>0$,
所以當$1<x<\frac{3}{2}$,M(x)>0,即F(x2)>0,
所以F(x)>0,即原不等式成立.(12分)
點評 本題考查了利用導數處理函數的單調性、最值問題,考查了分類討論思想、轉化思想、轉化思想,考查了運算能力,屬于難題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
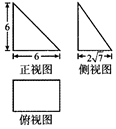 《九章算術》是我國古代內容極為豐富的數學名著,系統地總結了戰國、秦、漢時期的數學成就.書中將底面為長方形且有一條側棱與底面垂直的四棱錐稱之為“陽馬”,若某“陽馬”的三視圖如圖所示(單位:cm),則該陽馬的外接球的表面積為( )
《九章算術》是我國古代內容極為豐富的數學名著,系統地總結了戰國、秦、漢時期的數學成就.書中將底面為長方形且有一條側棱與底面垂直的四棱錐稱之為“陽馬”,若某“陽馬”的三視圖如圖所示(單位:cm),則該陽馬的外接球的表面積為( )| A. | 100π cm2 | B. | $\frac{500π}{3}$ cm2 | C. | 400π cm2 | D. | $\frac{4000π}{3}$ cm2 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com