
分析 (1)曲線C的參數方程消去參數α,能求出曲線C的普通方程;直線l的極坐標方程轉化為ρsinθ-ρcosθ=4,由此能求出直線l的直角坐標方程.
(2)設P(1+cosα,sinα),α∈[0,π]),求出P到直線l的距離,結合三角函數的性質能求出|PQ|的最小值.
解答 解:(1)∵曲線C的參數方程為$\left\{{\begin{array}{l}{x=1+cosα}\\{y=sinα}\end{array}}\right.$(α為參數,α∈[0,π]),
∴曲線C的普通方程為(x-1)2+y2=1.(y≥0).
∵直線l的極坐標方程為$ρ=\frac{4}{{\sqrt{2}sin({θ-\frac{π}{4}})}}$,
即ρsinθ-ρcosθ=4,
∴直線l的直角坐標方程為x-y+4=0.
(2)∵P為曲線C上任意一點,Q為直線l任意一點,
∴設P(1+cosα,sinα),α∈[0,π],
則P到直線l的距離:
d=$\frac{|1+cosα-sinα+4|}{\sqrt{2}}$=$\frac{|\sqrt{2}sin(α+\frac{3π}{4})+5|}{\sqrt{2}}$,
∵α∈[0,π],∴當α=$\frac{3π}{4}$時,dmin=$\frac{5-\sqrt{2}}{\sqrt{2}}$=$\frac{5\sqrt{2}-2}{2}$.
∴|PQ|的最小值為$\frac{5\sqrt{2}-2}{2}$.
點評 本題考查曲線的普通方程和直線的直角坐標方程的求法,考查線段長的最小值的求法,考查極坐標方程、直角坐標方程、參數方程的互化等基礎知識,考查推理論證能力、運算求解能力,考查化歸與轉化思想、函數與方程思想,是中檔題.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\left\{\begin{array}{l}x=2+t\\ y=1-t\end{array}\right.(t$為參數) | B. | $\left\{\begin{array}{l}x=1-\sqrt{t}\\ y=1+\sqrt{t}\end{array}\right.(t$為參數) | ||
| C. | $\left\{\begin{array}{l}x=3+t\\ y=-1-t\end{array}\right.(t$為參數) | D. | $\left\{\begin{array}{l}x=1-{t^2}\\ y=1+{t^2}\end{array}\right.(t$為參數) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
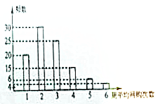 網購是當前民眾購物的新方式,某公司為改進營銷方式,隨機調查了100名市民,統計其周平均網購的次數,并整理得到如下的頻數分布直方圖.這100名市民中,年齡不超過40歲的有65人將所抽樣本中周平均網購次數不小于4次的市民稱為網購迷,且已知其中有5名市民的年齡超過40歲.
網購是當前民眾購物的新方式,某公司為改進營銷方式,隨機調查了100名市民,統計其周平均網購的次數,并整理得到如下的頻數分布直方圖.這100名市民中,年齡不超過40歲的有65人將所抽樣本中周平均網購次數不小于4次的市民稱為網購迷,且已知其中有5名市民的年齡超過40歲.| 網購迷 | 非網購迷 | 合計 | |
| 年齡不超過40歲 | |||
| 年齡超過40歲 | |||
| 合計 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.01 |
| k0 | 2.072 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| x | 4 | 5 | 6 | 7 | 8 |
| y | 12 | 10 | 9 | 8 | 6 |
| A. | -0.6 | B. | 0.6 | C. | -17.4 | D. | 17.4 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | Sn=2Tn | B. | Tn=2bn+1 | C. | Tn>an | D. | Tn<bn+1 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com