
| A. | (0,3) | B. | (-∞,0)∪(3,+∞) | C. | (1,2) | D. | (-∞,1)∪(2,+∞) |
分析 求出f(x)的解析式,判定f(x)的單調性和零點,利用單調性列不等式組解出x.
解答 解:當x<0時,-x>0,
∴f(x)=-6-f(-x)=-6-2-x+4=-2-$\frac{1}{{2}^{x}}$,
∴f(x)=$\left\{\begin{array}{l}{-2-\frac{1}{{2}^{x}},x<0}\\{{2}^{x}-4,x≥0}\end{array}\right.$,
∴f(x)<0在(-∞,0)上恒成立,
f(x)在[0,+∞)上是增函數,且f(2)=0,
∵f(3x-x2)<0,
∴3x-x2<2,
解得x<1或x>2,
故選D.
點評 本題考查了函數解析式的求解,函數單調性的判斷與應用,屬于中檔題.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 充分條件但不是必要條件 | B. | 必要條件但不是充分條件 | ||
| C. | 充要條件 | D. | 既不是充分條件,也不是必要條件 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
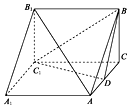 如圖,三棱柱ABC-A1B1C1中,AA1⊥面ABC,BC⊥AC,BC=AC=2,AA1=2,D為AC的中點.
如圖,三棱柱ABC-A1B1C1中,AA1⊥面ABC,BC⊥AC,BC=AC=2,AA1=2,D為AC的中點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{x}-\frac{1}{y}>0$ | B. | sinx-siny>0 | C. | ${({\frac{1}{2}})^x}-{({\frac{1}{2}})^y}<0$ | D. | lnx+lny>0 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com