日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

精英家教網 > 高中數學 > 題目詳情
5．設集合U={x|x2-3x+2=0，x∈R}，則集合U的子集的個數是4．

分析 解方程求出U的元素，從而求出其子集的個數即可．

解答 解：U={x|x2-3x+2=0，x∈R}={1，2}，
則集合U的子集的個數是：22=4，
故答案為：4．

點評 本題考查了求集合的子集問題，是一道基礎題．

練習冊系列答案
相關習題

科目：高中數學 來源： 題型：解答題

15．已知直線l：y=x+m，圓O：x2+y2-4=0，圓C：x2+y2+2ax-2ay+2a2-4a=0（0＜a≤4）．
（1）若a=3，圓O與圓C交于M，N兩點，試求線段|MN|的長．
（2）直線 l與圓C相切，且直線l在圓C心的下方，當0＜a≤4時，求m的取值范圍．

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

16．已知定義在R上的函數f（x），對任意x∈R，都有f（x+2）=f（x）+f（1）成立，若函數y=f（x-1）的圖象關于直線x=1對稱，則f（2015）=（　　）
A．-2B．0C．2D．2015

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

13．已知實數x，y滿足約束條件$\left\{\begin{array}{l}x-y+4≥0\\ x+y-2≤0\\ y-2≥0\end{array}$，則2y•（$\frac{1}{4}$）x的最小值是（　　）
A．1B．2C．8D．4

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

20．下列四組函數中，表示同一個函數的是（　　）
A．f（x）=|x+1|，g（x）=$\left\{\begin{array}{l}{x+1（x≥-1）}\\{-1-x（x＜-1）}\end{array}\right.$B．f（x）=$\frac{{x}^{2}-1}{x+1}$，g（x）=x-1
C．f（x）=$\sqrt{{x}^{2}}$，g（x）=（$\sqrt{x}$）2D．f（x）=x，g（x）=$\sqrt{{x}^{2}}$

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

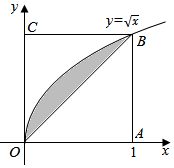10．如圖所示，在邊長為1的正方形OABC內任取一點P，用A表示事件“點P恰好自由曲線$y=\sqrt{x}$與直線x=1及x軸所圍成的曲邊梯形內”，B表示事件“點P恰好取自陰影部分內”，則P（B|A）等于（　　）
A．$\frac{1}{4}$B．$\frac{1}{5}$C．$\frac{1}{6}$D．$\frac{1}{7}$

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

17．若點（1，-3）在圓（x-2）2+（y+1）2=m的內部，則實數m的取值范圍是（　　）
A．0＜m＜10B．0＜m＜5C．m＞5D．m＜5

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

14．若函數f（x）=xlnx-ax2有兩個極值點，則實數a的取值范圍是（　　）
A．$（{0，\frac{1}{2}}）$B．$（{\frac{1}{2}，1}）$C．（1，2）D．（2，e）

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

15．已知函數f（x）=sin（π-ωx）cosωx+cos2ωx（ω＞0）的最小正周期為π．
（1）求ω的值；
（2）將函數y=f（x）的圖象上各點的橫坐標縮短到原來的$\frac{1}{2}$，縱坐標不變，得到函數y=g（x）的圖象，求函數g（x）在區間[0，$\frac{π}{16}$]上的最小值．

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： 黄色成人在线网站 | 亚洲免费一 | 亚洲午夜成激人情在线影院 | 免费的黄色影片 | 久久成人综合 | 一级日韩片| 亚洲女人天堂色在线7777 | 一区二区三区av | 韩国在线一区 | 久久久久久久香蕉 | 久久精品一级 | 欧美日韩毛片 | 精品欧美一区二区精品久久久 | 久久亚洲欧美日韩精品专区 | 能看的毛片 | 国产成人涩涩涩视频在线观看 | 欧美精品1 | 亚洲国产成人在线 | 在线观看亚洲一区 | 欧美日一区二区 | 国产精品中文字幕在线观看 | www.久久.com| 精品九九| 日韩欧美国产一区二区三区 | 国产精选久久 | 91在线观看免费 | 欧美一区二区激情三区 | 欧美日韩电影一区二区三区 | 一级欧美 | 欧美成年网站 | 国产精品一二三四区 | 欧美 日韩 高清 | 国产免费看 | 精品久久久久久久 | 欧美成人高清视频 | 日本一区二区视频 | 日本精品一区二区三区视频 | 久久精品国产亚洲blacked | 久草青青草| 免费国产成人 | 亚洲第一区在线 |