
分析 (1)由方程x2+y2-4=0與x2+y2+6x-6y+6=0消去二次項得,3x-3y+5=0,再求得圓心O到直線3x-3y+5=0的距離,由圓弦長、圓心距和圓的半徑之間關系得線段|MN|的長;
(2)由直線l與圓C相切,建立m與a的關系$\frac{{|{m-2a}|}}{{\sqrt{2}}}=2\sqrt{a}$,再由點C在直線l的上方,去掉絕對值,將m轉化為關于a二次函數求解.
解答 解:(1)當a=3時,C:x2+y2+6x-6y+6=0,由方程x2+y2-4=0與x2+y2+6x-6y+6=0消去二次項得,3x-3y+5=0,圓心O到直線3x-3y+5=0的距離為$d=\frac{{|{0-0+5}|}}{{\sqrt{9+9}}}=\frac{{5\sqrt{2}}}{6}$,∴$|{MN}|=2\sqrt{4-\frac{25}{18}}=\frac{{\sqrt{94}}}{3}$.
(2)∵x2+y2+2ax-2ay+2a2-4a=0,∴(x+a)2+(y-a)2=4a,∴圓心C(-a,a),半徑$r=2\sqrt{a}$,
圓心C(-a,a)到直線l的距離為$d=\frac{{|{-a-a+m}|}}{{\sqrt{2}}}=\frac{{|{m-2a}|}}{{\sqrt{2}}}$,
∵直線l與圓C2相切,∴d=r,即$\frac{{|{m-2a}|}}{{\sqrt{2}}}=2\sqrt{a}$,∴$m=2a±2\sqrt{2a}$,
∵直線l在圓心C的下方,∴$m=2a-2\sqrt{2a}={({\sqrt{2a}-1})^2}-1$,∵0<a≤4,
∴$m∈[{-1,8-4\sqrt{2}}]$.
點評 本題主要考查直線與圓的位置關系及其方程的應用,主要涉及了直線與圓相交,由圓心距,半徑和圓的弦長構成的直角三角形.


 第1卷單元月考期中期末系列答案
第1卷單元月考期中期末系列答案科目:高中數學 來源: 題型:解答題
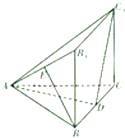 如圖,幾何體ABC-C1B1的底面ABC為等邊三角形,側面BB1C1C為矩形,B1B⊥平面ABC,E為邊AB1的中點,D在邊BC上移動.
如圖,幾何體ABC-C1B1的底面ABC為等邊三角形,側面BB1C1C為矩形,B1B⊥平面ABC,E為邊AB1的中點,D在邊BC上移動.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | f(λ)=$\frac{λ}{λ+2}$ | B. | f(λ)=$\frac{2λ}{λ+6}$ | C. | f(λ)=$\frac{3λ}{λ+7}$ | D. | f(λ)=$\frac{4λ}{λ+9}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| x(單位:千元) | 2 | 4 | 7 | 17 | 30 |
| y(單位:萬元) | 1 | 2 | 3 | 4 | 5 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題

查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com