
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
分析 設(shè)需要n天時間才能打穿$\frac{{2}^{n}-1}{2-1}$+$\frac{1-\frac{1}{{2}^{n}}}{1-\frac{1}{2}}$≥1000,化為:2n-$\frac{2}{{2}^{n}}$-999≥0,令f(n)=2n-$\frac{2}{{2}^{n}}$-999,利用函數(shù)零點(diǎn)存在定理與函數(shù)的單調(diào)性即可得出
解答 解:設(shè)需要n天時間才能打穿,則$\frac{{2}^{n}-1}{2-1}$+$\frac{1-\frac{1}{{2}^{n}}}{1-\frac{1}{2}}$≥1000,
化為:2n-$\frac{2}{{2}^{n}}$-999≥0,
令f(n)=2n-$\frac{2}{{2}^{n}}$-999,則f(10)=1024-$\frac{1}{512}$-999>0.
f(9)=512-$\frac{1}{256}$-999<0.
f(x)=${2}^{x}-\frac{2}{{2}^{x}}$-999,(x≥1).
∴f(x)在(9,10)內(nèi)存在一個零點(diǎn).
又函數(shù)f(x)在x≥1時單調(diào)遞增,因此f(x)在(9,10)內(nèi)存在唯一一個零點(diǎn).
∴需要10天時間才能打穿.
故選:C.
點(diǎn)評 本題考查了函數(shù)零點(diǎn)存在定理與函數(shù)的單調(diào)性、等比數(shù)列的通項(xiàng)公式與求和公式,考查了推理能力與計算能力,屬于中檔題.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:選擇題
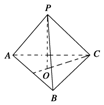 已知點(diǎn)P是正三角形ABC所在平面外一點(diǎn),PA=PB=PC=$\frac{2}{3}$,AB=1,則PC和平面ABC所成的角是( )
已知點(diǎn)P是正三角形ABC所在平面外一點(diǎn),PA=PB=PC=$\frac{2}{3}$,AB=1,則PC和平面ABC所成的角是( )| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | $3\sqrt{2}$ | B. | $4\sqrt{2}$ | C. | $5\sqrt{2}$ | D. | $7\sqrt{2}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\frac{25}{8}$ | B. | $\frac{25}{4}$ | C. | 25 | D. | $\frac{4}{25}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 向左平行移動$\frac{π}{3}$個單位長度 | B. | 向右平行移動$\frac{π}{3}$個單位長 | ||
| C. | 向左平行移動$\frac{π}{9}$個單位長度 | D. | 向右平行移動$\frac{π}{9}$個單位長度 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\overrightarrow{AB}$+$\overrightarrow{BA}$=$\overrightarrow{0}$ | |
| B. | 若|$\overrightarrow{a}$|=|$\overrightarrow{b}$|且$\overrightarrow{a}$∥$\overrightarrow{b}$,則$\overrightarrow{a}$=$\overrightarrow{b}$ | |
| C. | 若|$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{a}$+$\overrightarrow{b}$|,則$\overrightarrow{a}$⊥$\overrightarrow{b}$ | |
| D. | 若向量$\overrightarrow{b}$與向量$\overrightarrow{a}$共線,則有且只有一個實(shí)數(shù)λ,使得$\overrightarrow{b}$=λ$\overrightarrow{a}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 4 | B. | 6 | C. | 8 | D. | 9 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com