Question

5．如圖，平行四邊形PABC中，∠PAC=∠ABC=90°，PA=AB=2$\sqrt{3}$，AC=4，現把△PAC沿AC折起，使PA與平面ABC成60°角，設此時P在平面ABC上的投影為O點（O與B在AC的同側）．

（Ⅰ）求證：OB∥平面PAC；
（Ⅱ）試問：線段PA上是否在存在一點M，使得二面角M-BC-A的余弦值為$\frac{5\sqrt{37}}{37}$？若存在，指出M的位置，若不存在，請說明理由．

Answer 1

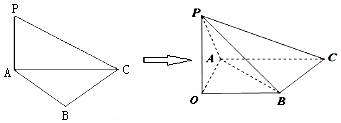
分析 （I）連接AO，證明CA⊥平面PAO，說明∠PAO是PA與平面ABC的角，通過證明OB∥AC，推出OB∥平面PAC．
（II）以O點為空間中坐標原點，OB、OA、OP所在軸為x、y、z軸，建立空間直角坐標系，求出相關點的坐標，平面ABC的一個法向量，設$M（{x_0}，{y_0}，{z_0}），\overrightarrow{PM}=（{x_0}，{y_0}，{z_0}-3）$，求出平面BCM的法向量，通過$cos＜\overrightarrow{m，}\overrightarrow n＞=\frac{5}{{\sqrt{37}}}$，解得$λ=\frac{1}{3}（λ=2舍去）$，說明存在線段PA上一點M，使得二面角M-BC-A的余弦值為$\frac{{5\sqrt{37}}}{37}$．

解答 解：（I）連接AO，∵PO⊥平面ABC，∴PO⊥CA．∵CA⊥PA，PA∩PO=P，
∴CA⊥平面PAO，CA⊥AO．∵∠PAO是PA與平面ABC的角，∴∠PAO=60°．
∵PA=2$\sqrt{3}$，∴OA=$\sqrt{3}$．
在直角△ABC中，∠BAC=30°，在△OAB中，∠OAB=90°-30^°=60^°，
∴OB⊥OA，從而有OB∥AC，∵OB?平面PAC，AC?平面PAC，
∴OB∥平面PAC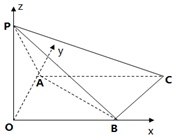

（II）由（I）得：以O點為空間中坐標原點，OB、OA、OP所在軸為x、y、z軸，
建立空間直角坐標系，可得$A（0，\sqrt{3}，0），B（3，0，0），C（4，\sqrt{3}，0），P（0，0，3）$．
取平面ABC的一個法向量為$\overrightarrow m=（0，0，1）$，
設$M（{x_0}，{y_0}，{z_0}），\overrightarrow{PM}=（{x_0}，{y_0}，{z_0}-3）$，$\overrightarrow{PA}=（0，\sqrt{3}，-3），\overrightarrow{PM}=λ\overrightarrow{PA}（0≤λ≤1）$，
∴$\left\{{\begin{array}{l}{{x_0}=0}\\{{y_0}=\sqrt{3}λ}\\{{z_0}=3-3λ}\end{array}}\right.$，$M（0，\sqrt{3}λ，3-3λ），\overrightarrow{BM}=（-3，\sqrt{3}λ，3-3λ）$，$\overrightarrow{BC}=（1，\sqrt{3}，0）$，
設平面BCM的法向量$\overrightarrow n=（x，y，z）$，$\left\{{\begin{array}{l}{\overrightarrow{BC}•\overrightarrow n=0}\\{\overrightarrow{BM}•\overrightarrow n=0}\end{array}}\right.$，當λ=1顯然不符合題意，
所以解得$\left\{{\begin{array}{l}{x=-\sqrt{3}y}\\{z=\frac{{\sqrt{3}（3+λ）}}{3（λ-1）}y}\end{array}}\right.$，取y=1，即$\overrightarrow n=（-\sqrt{3}，1，\frac{{\sqrt{3}（3+λ）}}{3（λ-1）}）$，$cos＜\overrightarrow{m，}\overrightarrow n＞=\frac{5}{{\sqrt{37}}}$，
解得$λ=\frac{1}{3}（λ=2舍去）$，所以M點是線段PA的三等分點，且靠近P點．
∴存在線段PA上一點M，使得二面角M-BC-A的余弦值為$\frac{{5\sqrt{37}}}{37}$．

點評 本題考查直線與平面垂直以及平行的判定定理的應用，二面角的平面角的求法與應用，考查空間想象能力以及計算能力．