
分析 (1)根據三角函數的定義求解即可.
(2)根據同角三角函數關系式求解.
解答 解:(1)角α的終邊上一點P(m,-$\sqrt{3}$)(m≠0),且cosα=$\frac{{\sqrt{2}m}}{4}$
設知$x=m,y=-\sqrt{3}$,
∴${r^2}=|OP{|^2}={(-\sqrt{3})^2}+{m^2}$(O為原點),
則$r=\sqrt{3+{m^2}}$.
∴$cosα=\frac{m}{r}=\frac{{\sqrt{2}m}}{4}=\frac{m}{{2\sqrt{2}}}$,
∴$r=\sqrt{3+{m^2}}=2\sqrt{2}$,
即3+m2=8,
解得$m=±\sqrt{5}$.
(2)由(1)可知:當$m=\sqrt{5}$時,$cosα=\frac{{\sqrt{10}}}{4}$,$sinα=\frac{{-\sqrt{6}}}{4}$,$tanα=\frac{sinα}{cosα}=-\frac{{\sqrt{15}}}{5}$;
當$m=-\sqrt{5}$時,$cosα=-\frac{{\sqrt{10}}}{4}$,$sinα=\frac{{-\sqrt{6}}}{4}$,$tanα=\frac{sinα}{cosα}=\frac{{\sqrt{15}}}{5}$.
點評 本題考查任意角的三角函數的定義和同角三角函數的運用,基本知識的考查.


 海淀黃岡名師導航系列答案
海淀黃岡名師導航系列答案 普通高中同步練習冊系列答案
普通高中同步練習冊系列答案 優翼小幫手同步口算系列答案
優翼小幫手同步口算系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
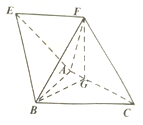 如圖,在四棱錐A-EFCB中,四邊形EFCB是梯形,EF∥BC且EF=$\frac{3}{4}$BC,△ABC是邊長為2的正三角形,頂點F在AC上射影為點G,且FG=$\sqrt{3}$,CF=$\frac{{\sqrt{21}}}{2}$,BF=$\frac{5}{2}$.
如圖,在四棱錐A-EFCB中,四邊形EFCB是梯形,EF∥BC且EF=$\frac{3}{4}$BC,△ABC是邊長為2的正三角形,頂點F在AC上射影為點G,且FG=$\sqrt{3}$,CF=$\frac{{\sqrt{21}}}{2}$,BF=$\frac{5}{2}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,已知正方形ABCD和矩形ACEF所在平面相互垂直,$AB=\sqrt{2},AF=1$,M在線段EF上.
如圖,已知正方形ABCD和矩形ACEF所在平面相互垂直,$AB=\sqrt{2},AF=1$,M在線段EF上.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 充分不必要條件 | B. | 必要不充分條件 | ||
| C. | 充分必要條件 | D. | 既不充分也不必要條件 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{4}$=1 | B. | $\frac{{x}^{2}}{7}$-$\frac{{y}^{2}}{9}$=1 | C. | $\frac{{x}^{2}}{8}$-$\frac{{y}^{2}}{8}$=1 | D. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ($\sqrt{2}$,+∞) | B. | ($\sqrt{2}$,2) | C. | (1,$\sqrt{2}$) | D. | (1,2) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com