
分析 (Ⅰ)求出原函數的導函數,得到f′(0),再求出f(0),由直線方程的點斜式得答案;
(Ⅱ)求出函數的導函數,因式分解可得:${f}^{′}(x)=\frac{1}{x+1}-\frac{1}{(ax+1)^{2}}$=$\frac{{a}^{2}x}{(x+1)(ax+1)}(x-\frac{1-2a}{{a}^{2}})$,然后對a分類討論可得函數f(x)在區間[0,1]上的單調性;
(Ⅲ)分別取a=0.5,a=0.4,結合(Ⅱ)中的單調性可得?n∈N*,$(1+\frac{1}{n})^{n+0.4}$<e<$(1+\frac{1}{n})^{n+0.5}$.取n=2016即可得到$(\frac{2017}{2016})^{2016.4}$<e<$(\frac{2017}{2016})^{2016.5}$.
解答 (Ⅰ)解:由${f}^{′}(x)=\frac{1}{x+1}-\frac{1}{(ax+1)^{2}}$,
得f′(0)=0,又f(0)=0,
∴切線方程為:y=0.
(Ⅱ)解:${f}^{′}(x)=\frac{1}{x+1}-\frac{1}{(ax+1)^{2}}$=$\frac{{a}^{2}x}{(x+1)(ax+1)}(x-\frac{1-2a}{{a}^{2}})$,
(1)當1-2a≤0,即$a≥\frac{1}{2}$時,f′(x)≥0,f(x)在[0,1]上單調遞增,
(2)當$\frac{1-2a}{{a}^{2}}≥1$,即$0<a≤\sqrt{2}-1$時,f′(x)≤0,f(x)在[0,1]上單調遞減,
(3)當$0<\frac{1-2a}{{a}^{2}}<1$,即$\sqrt{2}-2<a<\frac{1}{2}$時,
有:
| x | (0,$\frac{1-2a}{{a}^{2}}$) | $\frac{1-2a}{{a}^{2}}$ | ($\frac{1-2a}{{a}^{2}}$,1) |
| f′(x) | - | 0 | + |
| f(x) | 減函數 | 增函數 |
點評 本題考查利用導數研究函數的單調性,訓練了利用導數證明函數不等式,考查邏輯思維能力及推理論證能力,是中檔題.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{4}$=1 | B. | $\frac{{x}^{2}}{7}$-$\frac{{y}^{2}}{9}$=1 | C. | $\frac{{x}^{2}}{8}$-$\frac{{y}^{2}}{8}$=1 | D. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題

| A. | S>$\frac{1}{2}$ | B. | S>$\frac{3}{5}$ | C. | S>$\frac{7}{10}$ | D. | S>$\frac{4}{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
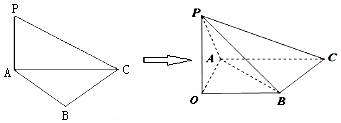
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | p∧q | B. | p∧¬q | C. | ¬p∧q | D. | ¬p∧¬q |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [-3,0] | B. | [-3,2] | C. | [0,2] | D. | [0,3] |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com