
| A. | 2 | B. | $\frac{4\sqrt{5}}{5}$ | C. | 3 | D. | $\sqrt{5}$ |
分析 由題意畫出圖形,把問題轉化為在拋物線y2=4x上找一點P,使得P到F的距離和到直線l1:2x-y+2=0的距離和最小,再用點到直線的距離公式求解.
解答 解:由拋物線y2=4x,得焦點坐標為F(1,0),準線方程為l2:x=-1,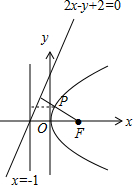
由拋物線定義知,P到直線l2的距離等于P到拋物線焦點F得距離.
故問題化為在拋物線y2=4x上找一點P,使得P到F的距離和到直線l1:2x-y+2=0的距離和最小.
最小值為F到l1:2x-y+2=0的距離,等于$\frac{|2-0+2|}{\sqrt{4+1}}=\frac{4\sqrt{5}}{5}$.
故選:B.
點評 本題考查拋物線的簡單性質,考查了數學轉化思想方法和數形結合的解題思想方法,是中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
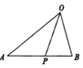 如圖,在△OAB,點P在邊AB上,且AP:PB=5:3,則$\overrightarrow{OP}$=( )
如圖,在△OAB,點P在邊AB上,且AP:PB=5:3,則$\overrightarrow{OP}$=( )| A. | $\frac{5}{8}$$\overrightarrow{OB}$+$\frac{3}{8}$$\overrightarrow{OA}$ | B. | $\frac{5}{8}$$\overrightarrow{OA}$+$\frac{3}{8}$$\overrightarrow{OB}$ | C. | $\frac{5}{8}$$\overrightarrow{OB}$-$\frac{3}{8}$$\overrightarrow{OA}$ | D. | $\frac{5}{8}$$\overrightarrow{OA}$-$\frac{3}{8}$$\overrightarrow{OB}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 逆時針方向勻速前跑 | B. | 順時針方向勻速前跑 | ||
| C. | 順時針方向勻速后退 | D. | 靜止不動 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com