
分析 (1)根據(jù)平面向量數(shù)量積的定義與夾角公式,即可求出$\overrightarrow{a}$、$\overrightarrow{b}$夾角的余弦值;
(2)【解法一】設(shè)$\overrightarrow{a}$、$\overrightarrow{b}$的夾角為θ,利用模長公式得出關(guān)于x的不等式(x2-1)+(2x-2)$\sqrt{2}$cosθ≥0,
討論x=1、x>1和x<1時,求出cosθ的值,從而求出θ的值;
【解法二】設(shè)a與b的夾角為θ,由|$\overrightarrow{a}$+x$\overrightarrow{b}$|≥|$\overrightarrow{a}$+$\overrightarrow{b}$得出不等式x2+2$\sqrt{2}$xcosθ-2$\sqrt{2}$cosθ-1≥0對一切實數(shù)x恒成立,
利用判別式△≤0求出cosθ的值,從而得出θ的值.
解答 解:(1)因為|$\overrightarrow{a}$|=$\sqrt{2}$,|$\overrightarrow{b}$|=1,|$\overrightarrow{a}$-$\overrightarrow{b}$|=2,
所以|$\overrightarrow{a}$-$\overrightarrow{b}$|2=4,
即$\overrightarrow{a}$2-2$\overrightarrow{a}$•$\overrightarrow{b}$+$\overrightarrow{b}$2=4,
2-2$\overrightarrow{a}$•$\overrightarrow{b}$+1=4,
所以$\overrightarrow{a}$•$\overrightarrow{b}$=-$\frac{1}{2}$.
設(shè)$\overrightarrow{a}$與$\overrightarrow{b}$的夾角為θ,
cosθ=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|×|\overrightarrow{b}|}$=$\frac{-\frac{1}{2}}{\sqrt{2}×1}$=-$\frac{\sqrt{2}}{4}$ …(4分)
(2)【解法一】令$\overrightarrow{a}$與$\overrightarrow{b}$的夾角為θ.
由|$\overrightarrow{a}$+x$\overrightarrow{b}$|≥|$\overrightarrow{a}$+$\overrightarrow{b}$|,得($\overrightarrow{a}$+x$\overrightarrow{b}$)2≥($\overrightarrow{a}$+$\overrightarrow{b}$)2,…(5分)
化為(x2-1)|$\overrightarrow{b}$|2+(2x-2)|$\overrightarrow{a}$|•|$\overrightarrow{b}$|cosθ≥0,
因為|$\overrightarrow{a}$|=$\sqrt{2}$,|$\overrightarrow{b}$|=1,
所以(x2-1)+(2x-2)$\sqrt{2}$cosθ≥0,…(6分)
當(dāng)x=1時,式子顯然成立; …(7分)
當(dāng)x>1時,cosθ≥-$\frac{{x}^{2}-1}{(2x-2)\sqrt{2}}$=-$\frac{x+1}{2\sqrt{2}}$,
由于-$\frac{x+1}{2\sqrt{2}}$<-$\frac{\sqrt{2}}{2}$,故cosθ≥-$\frac{\sqrt{2}}{2}$;
當(dāng)x<1時,cosθ≤-$\frac{{x}^{2}-1}{(2x-2)\sqrt{2}}$=-$\frac{x+1}{2\sqrt{2}}$,
由于-$\frac{x+1}{2\sqrt{2}}$>-$\frac{\sqrt{2}}{2}$,故cosθ≤-$\frac{\sqrt{2}}{2}$;
所以cosθ=-$\frac{\sqrt{2}}{2}$,解得θ=$\frac{3π}{4}$.…(12分)
【解法二】令$\overrightarrow{a}$與$\overrightarrow{b}$的夾角為θ,由|$\overrightarrow{a}$+x$\overrightarrow{b}$|≥|$\overrightarrow{a}$+$\overrightarrow{b}$|,
得($\overrightarrow{a}$+x$\overrightarrow{b}$)2≥($\overrightarrow{a}$+$\overrightarrow{b}$)2,…(5分)
因為|$\overrightarrow{a}$|=$\sqrt{2}$,|$\overrightarrow{b}$|=1,
所以x2+2$\sqrt{2}$xcosθ-2$\sqrt{2}$cosθ-1≥0,
對一切實數(shù)x恒成立,…(7分)
所以△=8cos2θ+8$\sqrt{2}$cosθ+4≤0,…(9分)
即($\sqrt{2}$cosθ+1)2≤0,故cosθ=-$\frac{{\sqrt{2}}}{2}$,…(11分)
因為θ∈[0,π],所以θ=$\frac{3}{4}$π.…(12分)
點評 本題考查了平面向量的數(shù)量積與夾角公式的由于問題,也考查了不等式恒成立問題,是綜合性題目.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | -x(1-x) | B. | x(1-x) | C. | -x(1+x) | D. | x(1+x) |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
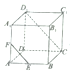 如圖,在正方體中ABCD-A1B1C1D1,E、F分別為AB,AA1的中點.求證:
如圖,在正方體中ABCD-A1B1C1D1,E、F分別為AB,AA1的中點.求證:查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
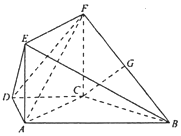 如圖,在梯形ABCD中,AB∥CD,AB=4,AD=DC=CB=2,四邊形ACFE是矩形,AE=1,平面ACFE⊥平面ABCD,點G是BF的中點.
如圖,在梯形ABCD中,AB∥CD,AB=4,AD=DC=CB=2,四邊形ACFE是矩形,AE=1,平面ACFE⊥平面ABCD,點G是BF的中點.查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com