
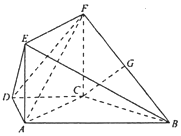
 如圖,在梯形ABCD中,AB∥CD,AB=4,AD=DC=CB=2,四邊形ACFE是矩形,AE=1,平面ACFE⊥平面ABCD,點G是BF的中點.
如圖,在梯形ABCD中,AB∥CD,AB=4,AD=DC=CB=2,四邊形ACFE是矩形,AE=1,平面ACFE⊥平面ABCD,點G是BF的中點.分析 (1)連結CE∩AF=O,連結OD,OG,推導出四邊形CDOG是平行四邊形,從而CG∥OD,由此能證明CG∥平面ADF.
(2)BC⊥平面ACFE,BE在平面ACFE上和射影為EC,BE與平面ACFE所成的角為∠BEC.由此能求出直線BE與平面ACFE所成角的正切值.
解答 證明:(1)連結CE∩AF=O,連結OD,OG,
∵在梯形ABCD中,AB∥CD,AB=4,AD=DC=CB=2,G是BF的中點,
∴OG$\underset{∥}{=}$$\frac{1}{2}$AB,CD$\underset{∥}{=}$$\frac{1}{2}$AB,∴OG$\underset{∥}{=}$CD,
∴四邊形CDOG是平行四邊形,
∴CG∥OD,
又OD?平面ADF,CG?平面ADF,
∴CG∥平面ADF.
解:(2)由(1)可知:BC⊥平面ACFE,BE在平面ACFE上和射影為EC,
BE與平面ACFE所成的角為∠BEC.
在△BCE中,∠BCE為直角,BC=2,
由勾股定理知:EC=3,
在△BCF中:tan∠BEC=$\frac{2}{3}$,
∴直線BE與平面ACFE所成角的正切值為$\frac{2}{3}$.
點評 本題考查線面平行的證明,考查直線與平面所成角的正切值的求法,是中檔題,解題時要認真審題,注意空間思維能力的培養.


 計算高手系列答案
計算高手系列答案科目:高中數學 來源: 題型:選擇題
| A. | (e,+∞) | B. | (1,e) | C. | (-∞,-e) | D. | (-e,-1) |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (2,$\frac{10}{3}$] | B. | [2,$\frac{10}{3}$] | C. | (2,+∞) | D. | [$\frac{10}{3}$,+∞] |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com