Question

7．設雙曲線C：$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1（a＞0，b＞0）左，右焦點為F₁，F₂，P是雙曲線C上的一點，PF₁與x軸垂直，△PF₁F₂的內切圓方程為（x+1）²+（y-1）²=1，則雙曲線方程為（　　）

• A． $\frac{x^2}{2}-\frac{y^2}{3}=1$
• B． ${x^2}-\frac{y^2}{2}=1$
• C． $\frac{x^2}{2}-{y^2}=1$
• D． ${x^2}-\frac{y^2}{3}=1$

Answer 1

分析 由題意可得：△PF₁F₂的內切圓圓心C（-1，1），半徑為r=1，由丨OF₁丨=2r=2，即可求得c，根據雙曲線的性質，求得丨PF₁丨=$\frac{{b}^{2}}{a}$，丨PF₂丨=2a+$\frac{{b}^{2}}{a}$，丨F₁F₂丨=2c=4，由內切圓的半徑公式徑r=$\frac{丨P{F}_{1}丨+丨{F}_{1}{F}_{2}丨-丨P{F}_{2}丨}{2}$=2-a=1，即可求得a，則b²=c²-a²=3求得雙曲線方程．

解答 解：，△PF₁F₂的內切圓方程為（x+1）²+（y-1）²=1，圓心C（-1，1），半徑為r=1，
∴丨OF₁丨=2r=2，
P（-2，$\frac{{b}^{2}}{a}$），
∴丨PF₁丨=$\frac{{b}^{2}}{a}$，由雙曲線的定義可知：丨PF₂丨=2a+$\frac{{b}^{2}}{a}$，丨F₁F₂丨=2c=4，
由三角形的內切圓的半徑r=$\frac{丨P{F}_{1}丨+丨{F}_{1}{F}_{2}丨-丨P{F}_{2}丨}{2}$=2-a=1，
則a=1，
由b²=c²-a²=3
∴雙曲線方程為：${x}^{2}-\frac{{y}^{2}}{3}=1$，
故選D．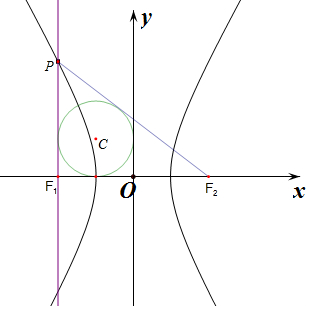

點評 本題考查雙曲線的簡單幾何性質，考查三角形的內切圓的半徑公式，考查數形結合思想，屬于中檔題．