
分析 (1)求導數,確定切線的斜率,可得切線方程;
(2)求出過點P,Q且與拋物線分別相切的直線方程,可得M的坐標,利用等比數列的定義進行證明.
解答 (1)解:由題意,y=2$\sqrt{x}$,y′=$\frac{1}{\sqrt{x}}$,x=1,y′=1,
∴過點P且與拋物線相切的直線方程為y-2=x-1,即x-y+1=0;
(2)證明:設P(x1,y1),Q(x2,y2),則過P的切線方程為y-y1=$\frac{1}{\sqrt{{x}_{1}}}$(x-x1),即y=$\frac{1}{\sqrt{{x}_{1}}}$x+$\sqrt{{x}_{1}}$,
同理過Q的切線方程為y=$\frac{1}{\sqrt{{x}_{2}}}$x+$\sqrt{{x}_{2}}$,可得M($\sqrt{{x}_{1}{x}_{2}}$,$\sqrt{{x}_{1}}$+$\sqrt{{x}_{2}}$),
∴|PF|=x1+1,|QF|=x2+1,|MF|2=($\sqrt{{x}_{1}{x}_{2}}$-1)2+($\sqrt{{x}_{1}}$+$\sqrt{{x}_{2}}$)2,
∴|MF|2=|PF||QF|,
∴|PF|,|MF|,|QF|依次成等比數列.
點評 本題考查拋物線的切線方程,考查等比數列的證明,綜合性強.


科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
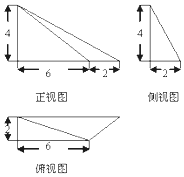
| A. | $\frac{56}{3}$ | B. | $\frac{112}{3}$ | C. | $\frac{119}{3}$ | D. | $\frac{128}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 若(a-2)(b-3)≠0,則a≠2或b≠3 | B. | 若(a-2)(b-3)≠0,則a≠2且b≠3 | ||
| C. | 若(a-2)(b-3)=0,則a≠2或b≠3 | D. | 若(a-2)(b-3)=0,則a≠2且b≠3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com