Question

5．在邊長為1的菱形ABCD中，∠ABC=60°，把菱形沿對角線AC折起，使折起后BD=$\frac{\sqrt{3}}{2}$，則二面角B-AC-D的余弦值為（　　）

• A． $\frac{1}{3}$
• B． $\frac{1}{2}$
• C． $\frac{2\sqrt{2}}{3}$
• D． $\frac{\sqrt{3}}{2}$

Answer 1

分析 如圖所示，在菱形ABCD中，對角線AC∩BD=O，由△ABC與△ACD都為等邊三角形，AB=1．可得AC⊥BD，OB=OD=$\frac{\sqrt{3}}{2}$，因此折起后∠BOD是二面角B-AC-D的平面角．利用等邊三角形的性質(zhì)即可得出結(jié)論．

解答 解：如圖所示，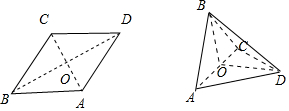
在菱形ABCD中，對角線AC∩BD=O，
由△ABC與△ACD都為等邊三角形，AB=1．
∴AC⊥BD，OB=OD=$\frac{\sqrt{3}}{2}$，
∴折起后∠BOD是二面角B-AC-D的平面角．
又BD=$\frac{\sqrt{3}}{2}$，
∴△BOD是等邊三角形，
∴∠BOD=$\frac{π}{3}$．
∴sin∠BOD=$\frac{\sqrt{3}}{2}$．
故選：D．

點評 本題考查了菱形與等邊三角形的性質(zhì)、二面角，考查了推理能力與計算能力，屬于中檔題．