
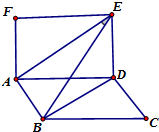
 如圖,矩形ADEF和矩形ABCD有公共邊AD.
如圖,矩形ADEF和矩形ABCD有公共邊AD.分析 (1)應用二面角的定義和線面垂直的判定定理和性質定理,結合解直角三角形,即可得到比值;
(2)連接BF,由AB⊥AD,AF⊥AD,可得∠BAF為二面角B-AD-F的平面角,且為60°,應用余弦定理可得BF,再由線面垂直的判定定理和性質定理,結合勾股定理,計算即可得到BE的值.
解答  解:(1)由題意可得,AB⊥AD,AF⊥AD,AB⊥AF,
解:(1)由題意可得,AB⊥AD,AF⊥AD,AB⊥AF,
即有AB⊥平面ADEF,可得AB⊥AE,
在直角三角形ABE中,cosα=$\frac{AE}{BE}$=$\frac{\sqrt{9+16}}{\sqrt{9+16+4}}$=$\frac{5}{\sqrt{29}}$;
同理在直角三角形DBE中,cosβ=$\frac{BD}{BE}$=$\frac{\sqrt{4+16}}{\sqrt{29}}$=$\frac{2\sqrt{5}}{\sqrt{29}}$;
則cosα:cosβ=$\sqrt{5}$:2;
(2)連接BF,由AB⊥AD,AF⊥AD,
可得∠BAF為二面角B-AD-F的平面角,且為60°,
由余弦定理可得BF2=BA2+FA2-2BA•FAcos60°=4a2+a2-2•2a•a•$\frac{1}{2}$
=3a2,
由線面垂直的判定定理可得AD⊥平面ABF,即有AD⊥BF,
AD∥EF,則EF⊥BF,
在直角三角形BEF中,BE2=BF2+EF2=3a2+4a2=7a2.
則BE=$\sqrt{7}$a.
故答案為:$\sqrt{5}$:2,$\sqrt{7}$a.
點評 本題考查空間二面角的求法和應用,同時考查線面垂直的判定和性質定理,考查運算能力,屬于中檔題.


 靈星計算小達人系列答案
靈星計算小達人系列答案科目:高中數學 來源: 題型:選擇題
| A. | A={x|x≥0},B=R,f:求算術平方根 | B. | A=R,B=R,f:取絕對值 | ||
| C. | A=R,B=R,f:取倒數 | D. | A=R+,B=R,f:求平方 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 焦點在x軸上的橢圓 | B. | 焦點在y軸上的橢圓 | ||
| C. | 過原點的直線 | D. | 圓心在原點的圓 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,-2)U(3,+∞) | B. | (2,3) | C. | {0,1,2} | D. | {1,2} |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com