
| A. | 焦點在x軸上的橢圓 | B. | 焦點在y軸上的橢圓 | ||
| C. | 過原點的直線 | D. | 圓心在原點的圓 |
分析 參數方程$\left\{{\begin{array}{l}{x=4sinθ}\\{y=5cosθ}\end{array}}\right.$,消去參數得到普通方程為$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{25}$=1,即可得出結論.
解答 解:參數方程$\left\{{\begin{array}{l}{x=4sinθ}\\{y=5cosθ}\end{array}}\right.$,消去參數得到普通方程為$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{25}$=1,
表示的曲線是焦點在y軸上的橢圓.
故選B.
點評 本題考查參數方程與普通方程的轉化,考查橢圓方程,比較基礎.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
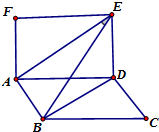 如圖,矩形ADEF和矩形ABCD有公共邊AD.
如圖,矩形ADEF和矩形ABCD有公共邊AD.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{{x}^{2}}{435600}$-$\frac{{y}^{2}}{564400}$=1(x>0) | B. | $\frac{{x}^{2}}{64{0}^{2}}$-$\frac{{y}^{2}}{48{0}^{2}}$=1(x>0) | ||
| C. | $\frac{{x}^{2}}{435600}$+$\frac{{y}^{2}}{564400}$=1 | D. | $\frac{{x}^{2}}{64{0}^{2}}$+$\frac{{y}^{2}}{48{0}^{2}}$=1 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com