
分析 (1)設等差數列{an}的公差為d,等比數列{bn}的公比為q,運用等差數列和等比數列的通項公式,列方程解方程可得d,q,即可得到所求通項公式;
(2)運用等比數列的求和公式,解方程可得公比,再由等差數列的通項公式和求和,計算即可得到所求和.
解答 解:(1)設等差數列{an}的公差為d,等比數列{bn}的公比為q,
a1=-1,b1=1,a2+b2=2,a3+b3=5,
可得-1+d+q=2,-1+2d+q2=5,
解得d=1,q=2或d=3,q=0(舍去),
則{bn}的通項公式為bn=2n-1,n∈N*;
(2)b1=1,T3=21,
可得1+q+q2=21,
解得q=4或-5,
當q=4時,b2=4,a2=2-4=-2,
d=-2-(-1)=-1,S3=-1-2-3=-6;
當q=-5時,b2=-5,a2=2-(-5)=7,
d=7-(-1)=8,S3=-1+7+15=21.
點評 本題考查等差數列和等比數列的通項公式和求和公式的運用,求出公差和公比是解題的關鍵,考查方程思想和化簡整理的運算能力,屬于基礎題.


科目:高中數學 來源: 題型:選擇題
| A. | -$\frac{7}{9}$ | B. | -$\frac{2}{9}$ | C. | $\frac{2}{9}$ | D. | $\frac{7}{9}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 在區間[-$\frac{π}{6}$,$\frac{π}{3}$]上單調遞減 | B. | 在區間[-$\frac{π}{6}$,$\frac{π}{3}$]上單調遞增 | ||
| C. | 在區間[-$\frac{π}{3}$,$\frac{π}{6}$]上單調遞減 | D. | 在區間[-$\frac{π}{3}$,$\frac{π}{6}$]上單調遞增 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
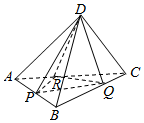 如圖,已知正四面體D-ABC(所有棱長均相等的三棱錐),P、Q、R分別為AB、BC、CA上的點,AP=PB,$\frac{BQ}{QC}$=$\frac{CR}{RA}$=2,分別記二面角D-PR-Q,D-PQ-R,D-QR-P的平面角為α、β、γ,則( )
如圖,已知正四面體D-ABC(所有棱長均相等的三棱錐),P、Q、R分別為AB、BC、CA上的點,AP=PB,$\frac{BQ}{QC}$=$\frac{CR}{RA}$=2,分別記二面角D-PR-Q,D-PQ-R,D-QR-P的平面角為α、β、γ,則( )| A. | γ<α<β | B. | α<γ<β | C. | α<β<γ | D. | β<γ<α |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
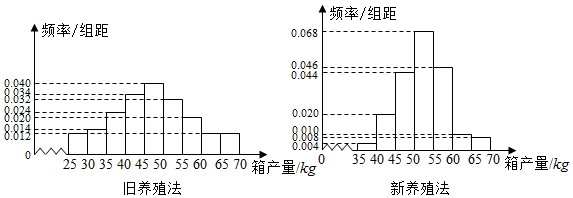
| 箱產量<50kg | 箱產量≥50kg | |
| 舊養殖法 | ||
| 新養殖法 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 已知{xn}是各項均為正數的等比數列,且x1+x2=3,x3-x2=2.
已知{xn}是各項均為正數的等比數列,且x1+x2=3,x3-x2=2.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com