
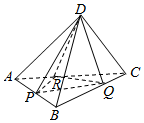
 如圖,已知正四面體D-ABC(所有棱長均相等的三棱錐),P、Q、R分別為AB、BC、CA上的點,AP=PB,$\frac{BQ}{QC}$=$\frac{CR}{RA}$=2,分別記二面角D-PR-Q,D-PQ-R,D-QR-P的平面角為α、β、γ,則( )
如圖,已知正四面體D-ABC(所有棱長均相等的三棱錐),P、Q、R分別為AB、BC、CA上的點,AP=PB,$\frac{BQ}{QC}$=$\frac{CR}{RA}$=2,分別記二面角D-PR-Q,D-PQ-R,D-QR-P的平面角為α、β、γ,則( )| A. | γ<α<β | B. | α<γ<β | C. | α<β<γ | D. | β<γ<α |
分析 解法一:如圖所示,建立空間直角坐標系.設底面△ABC的中心為O.不妨設OP=3.則O(0,0,0),P(0,-3,0),C(0,-6,0),D(0,0,6$\sqrt{2}$),Q$(\sqrt{3},2,0)$,R$(-2\sqrt{3},0,0)$,利用法向量的夾角公式即可得出二面角.
解法二:如圖所示,連接OP,OQ,OR,過點O分別作垂線:OE⊥PR,OF⊥PQ,OG⊥QR,垂足分別為E,F,G,連接DE,DF,DG..可得tanα=$\frac{OD}{OE}$.tanβ=$\frac{OD}{OF}$,tanγ=$\frac{OD}{OG}$.由已知可得:OE>OG>OF.即可得出.
解答 解法一:如圖所示,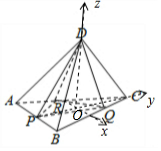 建立空間直角坐標系.設底面△ABC的中心為O.
建立空間直角坐標系.設底面△ABC的中心為O.
不妨設OP=3.則O(0,0,0),P(0,-3,0),C(0,-6,0),D(0,0,6$\sqrt{2}$),
Q$(\sqrt{3},2,0)$,R$(-2\sqrt{3},0,0)$,
$\overrightarrow{PR}$=$(-2\sqrt{3},3,0)$,$\overrightarrow{PD}$=(0,3,6$\sqrt{2}$),$\overrightarrow{PQ}$=($\sqrt{3}$,5,0),$\overrightarrow{QR}$=$(-3\sqrt{3},-2,0)$,
$\overrightarrow{QD}$=$(-\sqrt{3},-2,6\sqrt{2})$.
設平面PDR的法向量為$\overrightarrow{n}$=(x,y,z),則$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{PR}=0}\\{\overrightarrow{n}•\overrightarrow{PD}=0}\end{array}\right.$,可得$\left\{\begin{array}{l}{-2\sqrt{3}x+3y=0}\\{3y+6\sqrt{2}z=0}\end{array}\right.$,
可得$\overrightarrow{n}$=$(\sqrt{6},2\sqrt{2},-1)$,取平面ABC的法向量$\overrightarrow{m}$=(0,0,1).
則cos$<\overrightarrow{m},\overrightarrow{n}>$=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{-1}{\sqrt{15}}$,取α=arccos$\frac{1}{\sqrt{15}}$.
同理可得:β=arccos$\frac{3}{\sqrt{681}}$.γ=arccos$\frac{\sqrt{2}}{\sqrt{95}}$.
∵$\frac{1}{\sqrt{15}}$>$\frac{\sqrt{2}}{\sqrt{95}}$>$\frac{3}{\sqrt{681}}$.
∴α<γ<β.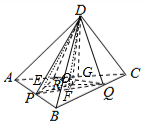
解法二:如圖所示,連接OP,OQ,OR,過點O分別作垂線:OE⊥PR,OF⊥PQ,OG⊥QR,垂足分別為E,F,G,連接DE,DF,DG.
設OD=h.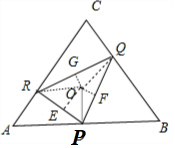
則tanα=$\frac{OD}{OE}$.
同理可得:tanβ=$\frac{OD}{OF}$,tanγ=$\frac{OD}{OG}$.
由已知可得:OE>OG>OF.
∴tanα<tanγ<tanβ,α,β,γ為銳角.
∴α<γ<β.
故選:B.
點評 本題考查了空間角、空間位置關系、正四面體的性質、法向量的夾角公式,考查了推理能力與計算能力,屬于難題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
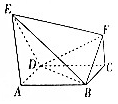 如圖,正方形ABCD的邊長為1,E,F是平面ABCD同一側的兩點,AE∥FC,AE⊥AB,AE=1,DE=$\sqrt{2}$,FC=$\frac{1}{2}$.
如圖,正方形ABCD的邊長為1,E,F是平面ABCD同一側的兩點,AE∥FC,AE⊥AB,AE=1,DE=$\sqrt{2}$,FC=$\frac{1}{2}$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 隨機變量ξ,η滿足η=2ξ+3,則其方差的關系為D(η)=4D(ξ) | |
| B. | 回歸分析中,R2的值越大,說明殘差平方和越小 | |
| C. | 畫殘差圖時,縱坐標一定為殘差,橫坐標一定為編號 | |
| D. | 回歸直線一定過樣本點中心 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 440 | B. | 330 | C. | 220 | D. | 110 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com