
分析 (1)根據a1=S1,a2=S2-a1結合原遞推式求得a1,a2的值;
(2)由數列遞推式可得an+1=2an+3,利用構造法即可證明數列{an+3}是等比數列,求出等比數列的通項公式可得數列{an}的通項公式;
(3)假設數列{S${\;}_{{n}_{k}}$}是等差數列,利用等差數列的定義借助于反證法進行證明.
解答 (1)解:由Sn=2an-3n(n∈N*)得到:
a1=S1=2a1-3,解得a1=3.
則a2=S2-a1=2a2-3×2-3,解得a2=9.
∴a1=3,a2=9;
(2)證明:∵Sn=2an-3n(n∈N*),
∴Sn+1=2an+1-3(n+1)(n∈N*),
∴an+1=2an+1-2an-3,即an+1=2an+3,
∴$\frac{{a}_{n+1}+3}{{a}_{n}+3}$=2,
則數列{an+3}是等比數列,
∴a1=3,a1+3=6,an+3=6•2n-1=3•2n,
∴an=3•2n-3;
(3)解:數列{S${\;}_{{n}_{k}}$}不是等差數列,理由如下:
假設數列{S${\;}_{{n}_{k}}$}是等差數列.
由(2)知,an=3•2n-3,則Sn=2an-3n=3•2n+1-3n-6.
∵數列{nk}是等差數列,
∴2n2=n1+n3,
∵數列{S${\;}_{{n}_{k}}$}是等差數列,
∴2S${\;}_{{n}_{2}}$=S${\;}_{{n}_{1}}$+S${\;}_{{n}_{2}}$,
即2(3•2${\;}^{{n}_{2}+1}$-3n2-6)=3•2${\;}^{{n}_{1}+1}$-3n1-6+3•2${\;}^{{n}_{3}+1}$-3n3-6
=3(2${\;}^{{n}_{1}+1}$+2${\;}^{{n}_{3}+1}$)-3(n1+n3)-12=3(2${\;}^{{n}_{1}+1}$+2${\;}^{{n}_{3}+1}$)-6n2-12.
整理,得2${\;}^{{n}_{2}+1}$=2${\;}^{{n}_{1}}$+2${\;}^{{n}_{3}}$,即$2•{2}^{\frac{{n}_{1}+{n}_{3}}{2}}$=2${\;}^{{n}_{1}}$+2${\;}^{{n}_{3}}$,
∵2${\;}^{{n}_{1}}$+2${\;}^{{n}_{3}}$>2$\sqrt{{2}^{{n}_{1}}•{2}^{{n}_{3}}}$=$2•{2}^{\frac{{n}_{1}+{n}_{3}}{2}}$,
∴$2•{2}^{\frac{{n}_{1}+{n}_{3}}{2}}$=2${\;}^{{n}_{1}}$+2${\;}^{{n}_{3}}$ 不成立.
故數列{S${\;}_{{n}_{k}}$}不是等差數列.
點評 本題考查等差數列與等比數列的通項公式,考查等比關系的確定,考查邏輯思維能力與推理論證能力,是中檔題.


 中考解讀考點精練系列答案
中考解讀考點精練系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 分組 | 頻數 | 頻率 |
| [60,70) | ③ | 0.16 |
| [70,80) | 14 | ② |
| [80,90) | 16 | 0.32 |
| [90,100] | ① | 0.24 |
| 合計 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
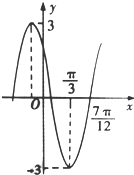 已知函數f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分圖象如圖所示,則曲線f(x)在(0,f(0))處在的切線方程為6$\sqrt{3}$x+2y-3=0.
已知函數f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分圖象如圖所示,則曲線f(x)在(0,f(0))處在的切線方程為6$\sqrt{3}$x+2y-3=0.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com