
分析 由題意離心率可得a與c,b與c的關系,代入橢圓方程,和直線方程聯立,利用弦長公式列式求得c,則橢圓方程可求.
解答 解:由$e=\frac{c}{a}=\frac{2}{3}$,得${a}^{2}=\frac{9}{4}{c}^{2}$,${b}^{2}={a}^{2}-{c}^{2}=\frac{5}{4}{c}^{2}$,
則橢圓方程為$\frac{{x}^{2}}{\frac{9}{4}{c}^{2}}+\frac{{y}^{2}}{\frac{5}{4}{c}^{2}}=1$,即20x2+36y2=45c2.
∵直線l過右焦點F,且傾斜角為60°,
∴直線l的方程為y=$\sqrt{3}$(x-c),
聯立$\left\{\begin{array}{l}{y=\sqrt{3}x-\sqrt{3}c}\\{20{x}^{2}+36{y}^{2}=45{c}^{2}}\end{array}\right.$,消去y得:128x2-216cx+63c2=0.
設A(x1,y1),B(x2,y2),
則${x}_{1}+{x}_{2}=\frac{216c}{128},{x}_{1}{x}_{2}=\frac{63{c}^{2}}{128}$,
∴|AB|=$\sqrt{1+(\sqrt{3})^{2}}•\sqrt{(\frac{216c}{128})^{2}-\frac{252{c}^{2}}{128}}$=$\frac{15}{4}$,解得c2=4.
∴橢圓方程為:$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{5}=1$.
點評 本題考查橢圓的簡單性質,考查了弦長公式的應用,考查計算能力,是中檔題.


科目:高中數學 來源: 題型:解答題
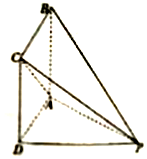 如圖,四棱錐P-ABCD的底面ABCD是正方形,PD⊥平面ABCD.
如圖,四棱錐P-ABCD的底面ABCD是正方形,PD⊥平面ABCD.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | -$\frac{π}{3}$ | D. | -$\frac{π}{6}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com