
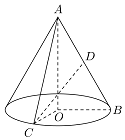
 如圖,在Rt△AOB中,$∠OAB=\frac{π}{6}$,斜邊AB=4,D是AB中點,現將Rt△AOB以
如圖,在Rt△AOB中,$∠OAB=\frac{π}{6}$,斜邊AB=4,D是AB中點,現將Rt△AOB以分析 (1)由圓錐的側面積S側=πrl,能求出結果.
(2)取OB的中點E,連結DE、CE,則DE∥AO,∴DE⊥平面BOC,∠DCE是直線CD與平面BOC所成的角,由此能求出直線CD與平面BOC所成角的大小.
解答 解:(1)∵在Rt△AOB中,$∠OAB=\frac{π}{6}$,斜邊AB=4,D是AB中點,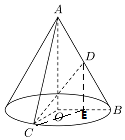
將Rt△AOB以直角邊AO為軸旋轉一周得到一個圓錐,點C為圓錐底面圓周上一點,且∠BOC=90°,
∴圓錐的側面積S側=πrl=2×4×π=8π.
(2)取OB的中點E,連結DE、CE,
則DE∥AO,∴DE⊥平面BOC,
∴∠DCE是直線CD與平面BOC所成的角,
在Rt△DEC中,CE=$\sqrt{5}$,DE=$\sqrt{3}$,
tan$∠DCE=\frac{\sqrt{3}}{\sqrt{5}}$=$\frac{\sqrt{15}}{5}$,
∴$∠DCE=arctan\frac{\sqrt{15}}{5}$.
∴直線CD與平面BOC所成角的大小為arctan$\frac{\sqrt{15}}{5}$.
點評 本題考查圓錐的側面積的求法,考查直線與平面所成角的大小的求法,是中檔題,解題時要認真審題,注意空間思維能力的培養.


 課時訓練江蘇人民出版社系列答案
課時訓練江蘇人民出版社系列答案 黃岡經典趣味課堂系列答案
黃岡經典趣味課堂系列答案 啟東小題作業本系列答案
啟東小題作業本系列答案科目:高中數學 來源: 題型:解答題
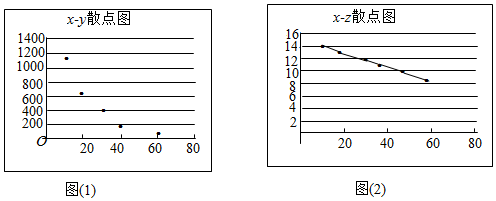
| 定價x(元/kg) | 10 | 20 | 30 | 40 | 50 | 60 |
| 年銷量y(kg) | 1150 | 643 | 424 | 262 | 165 | 86 |
| z=2lny | 14.1 | 12.9 | 12.1 | 11.1 | 10.2 | 8.9 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
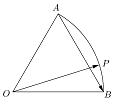 如圖,已知半徑為1的扇形AOB,∠AOB=60°,P為弧$\widehat{AB}$上的一個動點,則$\overrightarrow{OP}•\overrightarrow{AB}$取值范圍是[$-\frac{1}{2}$,$\frac{1}{2}$].
如圖,已知半徑為1的扇形AOB,∠AOB=60°,P為弧$\widehat{AB}$上的一個動點,則$\overrightarrow{OP}•\overrightarrow{AB}$取值范圍是[$-\frac{1}{2}$,$\frac{1}{2}$].查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
 如圖,有一直角墻角,兩邊的長度足夠長,若P處有一棵樹與兩墻的距離分別是4m和am(0<a<12),不考慮樹的粗細.現用16m長的籬笆,借助墻角圍成一個矩形花圃ABCD.設此矩形花圃的最大面積為u,若將這棵樹圍在矩形花圃內,則函數u=f(a)(單位m2)的圖象大致是( )
如圖,有一直角墻角,兩邊的長度足夠長,若P處有一棵樹與兩墻的距離分別是4m和am(0<a<12),不考慮樹的粗細.現用16m長的籬笆,借助墻角圍成一個矩形花圃ABCD.設此矩形花圃的最大面積為u,若將這棵樹圍在矩形花圃內,則函數u=f(a)(單位m2)的圖象大致是( )| A. |  | B. | 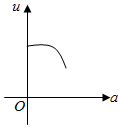 | C. | 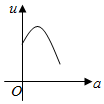 | D. | 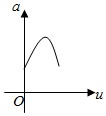 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com