
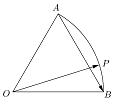
 如圖,已知半徑為1的扇形AOB,∠AOB=60°,P為弧$\widehat{AB}$上的一個動點,則$\overrightarrow{OP}•\overrightarrow{AB}$取值范圍是[$-\frac{1}{2}$,$\frac{1}{2}$].
如圖,已知半徑為1的扇形AOB,∠AOB=60°,P為弧$\widehat{AB}$上的一個動點,則$\overrightarrow{OP}•\overrightarrow{AB}$取值范圍是[$-\frac{1}{2}$,$\frac{1}{2}$]. 分析 結合圖形,將$\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}$代入$\overrightarrow{OP}•\overrightarrow{AB}$進行數量積的運算,并代入∠BOP=60°-∠AOP進行化簡即可得出$\overrightarrow{OP}•\overrightarrow{AB}=sin(∠AOP-30°)$,這樣,根據0°≤∠AOP≤60°即可求出sin(∠AOP-30°)的范圍,即求出$\overrightarrow{OP}•\overrightarrow{AB}$的取值范圍.
解答 解:$\overrightarrow{OP}•\overrightarrow{AB}=\overrightarrow{OP}•(\overrightarrow{OB}-\overrightarrow{OA})$
=$\overrightarrow{OP}•\overrightarrow{OB}-\overrightarrow{OP}•\overrightarrow{OA}$
=cos∠BOP-cos∠AOP
=cos(60°-∠AOP)-cos∠AOP
=$\frac{1}{2}cos∠AOP+\frac{\sqrt{3}}{2}sin∠AOP-cos∠AOP$
=$\frac{\sqrt{3}}{2}sin∠AOP-\frac{1}{2}cos∠AOP$
=sin(∠AOP-30°);
0°≤∠AOP≤60°;
∴-30°≤∠AOP-30°≤30°;
∴$-\frac{1}{2}≤sin(∠AOP-30°)≤\frac{1}{2}$;
∴$\overrightarrow{OP}•\overrightarrow{AB}$的取值范圍為$[-\frac{1}{2},\frac{1}{2}]$.
故答案為:[$-\frac{1}{2},\frac{1}{2}$].
點評 考查向量減法的幾何意義,向量數量積的運算及計算公式,兩角和差的正余弦公式,以及不等式的性質,熟悉正弦函數的圖象.


科目:高中數學 來源: 題型:選擇題
| A. | [$\frac{9}{5}$,3] | B. | (-∞,3] | C. | [3,+∞) | D. | (2,3] |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
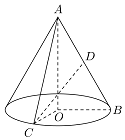 如圖,在Rt△AOB中,$∠OAB=\frac{π}{6}$,斜邊AB=4,D是AB中點,現將Rt△AOB以
如圖,在Rt△AOB中,$∠OAB=\frac{π}{6}$,斜邊AB=4,D是AB中點,現將Rt△AOB以查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 充分非必要條件 | B. | 必要非充分條件 | ||
| C. | 充要條件 | D. | 既非充分也非必要條件 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com