
分析 (1)由條件利用正弦定理、兩個向量的數量積公式、三角恒等變換化簡函數f(x)的解析式.
(2)利用正弦函數的單調性求得f(x)的單調區間,并求出x的值.
解答 解:(1)由正弦定理有$\frac{BC}{sinx}$=$\frac{1}{sin\frac{2π}{3}}$=$\frac{AD}{sin(\frac{π}{3}-x)}$
∴BC=$\frac{1}{sin\frac{2π}{3}}$•sinx,AB=$\frac{sin(\frac{π}{3}-x)}{sin\frac{2π}{3}}$,
∴$f(x)=\overrightarrow{AB}•\overrightarrow{BC}$=$\frac{4}{3}$sinx•sin($\frac{π}{3}$-x)•$\frac{1}{2}$=$\frac{2}{3}$($\frac{\sqrt{3}}{2}$cosx-$\frac{1}{2}$sinx)sinx=$\frac{1}{3}$sin(2x+$\frac{π}{6}$)-$\frac{1}{6}$,
其定義域為(0,$\frac{π}{3}$)
(2)∵-$\frac{π}{2}$+2kπ≤2x+$\frac{π}{6}$≤$\frac{π}{2}$+2kπ,k∈Z,
∴-$\frac{π}{3}$+kπ≤x≤$\frac{π}{6}$+kπ,k∈Z,
∵x∈(0,$\frac{π}{3}$)
∴遞增區間$(0,\frac{π}{6}]$,
∵方程$f(x)=\frac{1}{6}$=$\frac{1}{3}$sin(2x+$\frac{π}{6}$)-$\frac{1}{6}$,
∴sin(2x+$\frac{π}{6}$)=1,
解得$x=\frac{π}{6}$.
點評 本題考查了正弦定理、數量積運算、三角形的內角和定理、正弦函數的單調性,考查了推理能力和計算能力,屬于中檔題.


 學練快車道口算心算速算天天練系列答案
學練快車道口算心算速算天天練系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
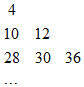 設數列{an}是集合{x|x=3s+3t,s<t且s,t∈N}中所有的數從小到大排列成的數列,即a1=4,a2=10,a3=12,a4=28,a5=30,a6=36,…,將數列{an}中各項按照上小下大,左小右大的原則排成如圖的等腰直角三角形數表,則a15的值為324.
設數列{an}是集合{x|x=3s+3t,s<t且s,t∈N}中所有的數從小到大排列成的數列,即a1=4,a2=10,a3=12,a4=28,a5=30,a6=36,…,將數列{an}中各項按照上小下大,左小右大的原則排成如圖的等腰直角三角形數表,則a15的值為324.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
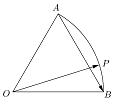 如圖,已知半徑為1的扇形AOB,∠AOB=60°,P為弧$\widehat{AB}$上的一個動點,則$\overrightarrow{OP}•\overrightarrow{AB}$取值范圍是[$-\frac{1}{2}$,$\frac{1}{2}$].
如圖,已知半徑為1的扇形AOB,∠AOB=60°,P為弧$\widehat{AB}$上的一個動點,則$\overrightarrow{OP}•\overrightarrow{AB}$取值范圍是[$-\frac{1}{2}$,$\frac{1}{2}$].查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 當x=e時,f(x)取得最小值 | B. | f(x)最大值為1 | ||
| C. | 不等式f(x)<0的解集是(1,e) | D. | 當$\frac{1}{e}$<x<1時,f(x)>0 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com