
分析 由題意可得$\left\{\begin{array}{l}{\frac{a}{2}+\frac{1}{2}lna=ta}\\{\frac{b}{2}+\frac{1}{2}lnb=tb}\end{array}\right.$,即$\frac{x}{2}+\frac{1}{2}lnx=tx$在(0,+∞)上有2個不等實數根,故函數y=$\frac{x}{2}+\frac{1}{2}lnx$的圖象與函數y=tx的圖象在(0,+∞)上有兩個不同的交點.求得t的范圍.
解答 解:函數$f(x)=\frac{x}{2}+ln\sqrt{x}$在(0,+∞)為增函數,某區間[a,b]上的值域為[ta,tb],
可得$\left\{\begin{array}{l}{\frac{a}{2}+\frac{1}{2}lna=ta}\\{\frac{b}{2}+\frac{1}{2}lnb=tb}\end{array}\right.$,即$\frac{x}{2}+\frac{1}{2}lnx=tx$,變形為$\frac{1}{2}lnx=x(t-\frac{1}{2})$在(0,+∞)上有2個不等實數根,
故函數y=$\frac{1}{2}lnx$的圖象與函數y=(t-$\frac{1}{2}$)x的圖象在(0,+∞)上有兩個不同的交點,
∴t-$\frac{1}{2}$>0,解得:t$>\frac{1}{2}$
令F(x)=$\frac{x}{2}+\frac{1}{2}lnx$-tx
則F′(x)=$\frac{1}{2x}+\frac{1}{2}-t$
令F′(x)=0,解得:x=$\frac{1}{2t-1}$
故當x=$\frac{1}{2t-1}$是函數y=$\frac{1}{2}lnx$的圖象與函數y=(t-$\frac{1}{2}$)x的圖象切點.
故得$(t-\frac{1}{2})\frac{1}{2t-1}=\frac{1}{2}ln(\frac{1}{2t-1})$,
解得:t=$\frac{1+e}{2e}$
故得t的取值范圍是$\frac{1}{2}<t<\frac{1+e}{2e}$.
故答案為:($\frac{1}{2}$,$\frac{1+e}{2e}$)
點評 本題主要考查求函數的定義域和值域,構造函數的思想,屬于中檔題.


科目:高中數學 來源: 題型:解答題
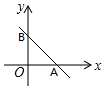 直線3x+4y-12=0與兩坐標軸的交點為A,B,其中點A在x軸上,點B在y軸上.
直線3x+4y-12=0與兩坐標軸的交點為A,B,其中點A在x軸上,點B在y軸上.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{{2\sqrt{10}}}{5}$ | B. | $\frac{{\sqrt{10}}}{10}$ | C. | $\frac{{\sqrt{10}}}{5}$ | D. | $\frac{{3\sqrt{10}}}{10}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [$\frac{9}{5}$,3] | B. | (-∞,3] | C. | [3,+∞) | D. | (2,3] |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com