
| A. | 160 | B. | 163 | C. | 166 | D. | 170 |
分析 由數據求得樣本中心點,由回歸直線方程必過樣本中心點,代入即可求得$\widehat{a}$,將x=24代入回歸直線方程即可估計其身高.
解答 解:由線性回歸方程為$\widehat{y}$=4x+$\widehat{a}$,
則$\overline{x}$=$\frac{1}{10}$$\sum_{i=1}^{10}$xi=22.5,$\overline{y}$=$\frac{1}{10}$$\sum_{i=1}^{10}$yi=160,
則數據的樣本中心點(22.5,160),
由回歸直線方程樣本中心點,則$\widehat{a}$=$\widehat{y}$-4x=160-4×22.5=70,
∴回歸直線方程為$\widehat{y}$=4x+70,
當x=24時,$\widehat{y}$=4×24+70=166,
則估計其身高為166,
故選C.
點評 本題考查回歸直線方程的求法及回歸直線方程的應用,考查計算能力,屬于基礎題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 在區間[-$\frac{π}{6}$,$\frac{π}{3}$]上單調遞減 | B. | 在區間[-$\frac{π}{6}$,$\frac{π}{3}$]上單調遞增 | ||
| C. | 在區間[-$\frac{π}{3}$,$\frac{π}{6}$]上單調遞減 | D. | 在區間[-$\frac{π}{3}$,$\frac{π}{6}$]上單調遞增 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
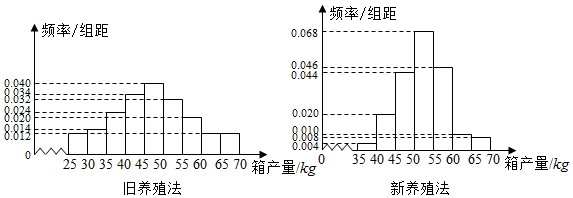
| 箱產量<50kg | 箱產量≥50kg | |
| 舊養殖法 | ||
| 新養殖法 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (0,1]∪[2$\sqrt{3}$,+∞) | B. | (0,1]∪[3,+∞) | C. | (0,$\sqrt{2}$)∪[2$\sqrt{3}$,+∞) | D. | (0,$\sqrt{2}$]∪[3,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
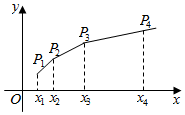 已知{xn}是各項均為正數的等比數列,且x1+x2=3,x3-x2=2.
已知{xn}是各項均為正數的等比數列,且x1+x2=3,x3-x2=2.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
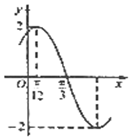 已知函數$f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<\frac{π}{2})$的部分圖象如圖所示,下列說法正確的有( )個
已知函數$f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<\frac{π}{2})$的部分圖象如圖所示,下列說法正確的有( )個| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com