
| A. | (0,1]∪[2$\sqrt{3}$,+∞) | B. | (0,1]∪[3,+∞) | C. | (0,$\sqrt{2}$)∪[2$\sqrt{3}$,+∞) | D. | (0,$\sqrt{2}$]∪[3,+∞) |
分析 根據題意,由二次函數的性質分析可得:y=(mx-1)2 為二次函數,在區間(0,$\frac{1}{m}$)為減函數,($\frac{1}{m}$,+∞)為增函數,分2種情況討論:①、當0<m≤1時,有$\frac{1}{m}$≥1,②、當m>1時,有$\frac{1}{m}$<1,結合圖象分析兩個函數的單調性與值域,可得m的取值范圍,綜合可得答案.
解答 解:根據題意,由于m為正數,y=(mx-1)2 為二次函數,在區間(0,$\frac{1}{m}$)為減函數,($\frac{1}{m}$,+∞)為增函數,
函數y=$\sqrt{x}$+m為增函數,
分2種情況討論:
①、當0<m≤1時,有$\frac{1}{m}$≥1,
在區間[0,1]上,y=(mx-1)2 為減函數,且其值域為[(m-1)2,1],
函數y=$\sqrt{x}$+m為增函數,其值域為[m,1+m],
此時兩個函數的圖象有1個交點,符合題意;
②、當m>1時,有$\frac{1}{m}$<1,
y=(mx-1)2 在區間(0,$\frac{1}{m}$)為減函數,($\frac{1}{m}$,1)為增函數,
函數y=$\sqrt{x}$+m為增函數,其值域為[m,1+m],
若兩個函數的圖象有1個交點,則有(m-1)2≥1+m,
解可得m≤0或m≥3,
又由m為正數,則m≥3;
綜合可得:m的取值范圍是(0,1]∪[3,+∞);
故選:B.
點評 本題考查函數圖象的交點問題,涉及函數單調性的應用,關鍵是確定實數m的分類討論.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 160 | B. | 163 | C. | 166 | D. | 170 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
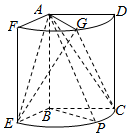 如圖,幾何體是圓柱的一部分,它是由矩形ABCD(及其內部)以AB邊所在直線為旋轉軸旋轉120°得到的,G是$\widehat{DF}$的中點.
如圖,幾何體是圓柱的一部分,它是由矩形ABCD(及其內部)以AB邊所在直線為旋轉軸旋轉120°得到的,G是$\widehat{DF}$的中點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{2}{3}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com