
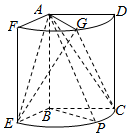
 如圖,幾何體是圓柱的一部分,它是由矩形ABCD(及其內部)以AB邊所在直線為旋轉軸旋轉120°得到的,G是$\widehat{DF}$的中點.
如圖,幾何體是圓柱的一部分,它是由矩形ABCD(及其內部)以AB邊所在直線為旋轉軸旋轉120°得到的,G是$\widehat{DF}$的中點.分析 (Ⅰ)由已知利用線面垂直的判定可得BE⊥平面ABP,得到BE⊥BP,結合∠EBC=120°求得∠CBP=30°;
(Ⅱ)法一、取$\widehat{EC}$的中點H,連接EH,GH,CH,可得四邊形BEGH為菱形,取AG中點M,連接EM,CM,EC,得到EM⊥AG,CM⊥AG,說明∠EMC為所求二面角的平面角.求解三角形得二面角E-AG-C的大小.
法二、以B為坐標原點,分別以BE,BP,BA所在直線為x,y,z軸建立空間直角坐標系.求出A,E,G,C的坐標,進一步求出平面AEG與平面ACG的一個法向量,由兩法向量所成角的余弦值可得二面角E-AG-C的大小.
解答 解:(Ⅰ)∵AP⊥BE,AB⊥BE,且AB,AP?平面ABP,AB∩AP=A,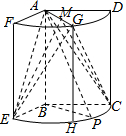
∴BE⊥平面ABP,又BP?平面ABP,
∴BE⊥BP,又∠EBC=120°,
因此∠CBP=30°;
(Ⅱ)解法一、
取$\widehat{EC}$的中點H,連接EH,GH,CH,
∵∠EBC=120°,∴四邊形BECH為菱形,
∴AE=GE=AC=GC=$\sqrt{{3}^{2}+{2}^{2}}=\sqrt{13}$.
取AG中點M,連接EM,CM,EC,
則EM⊥AG,CM⊥AG,
∴∠EMC為所求二面角的平面角.
又AM=1,∴EM=CM=$\sqrt{13-1}=2\sqrt{3}$.
在△BEC中,由于∠EBC=120°,
由余弦定理得:EC2=22+22-2×2×2×cos120°=12,
∴$EC=2\sqrt{3}$,因此△EMC為等邊三角形,
故所求的角為60°.
解法二、以B為坐標原點,分別以BE,BP,BA所在直線為x,y,z軸建立空間直角坐標系.
由題意得:A(0,0,3),E(2,0,0),G(1,$\sqrt{3}$,3),C(-1,$\sqrt{3}$,0),
故$\overrightarrow{AE}=(2,0,-3)$,$\overrightarrow{AG}=(1,\sqrt{3},0)$,$\overrightarrow{CG}=(2,0,3)$.
設$\overrightarrow{m}=({x}_{1},{y}_{1},{z}_{1})$為平面AEG的一個法向量,
由$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{AE}=0}\\{\overrightarrow{m}•\overrightarrow{AG}=0}\end{array}\right.$,得$\left\{\begin{array}{l}{2{x}_{1}-3{z}_{1}=0}\\{{x}_{1}+\sqrt{3}{y}_{1}=0}\end{array}\right.$,取z1=2,得$\overrightarrow{m}=(3,-\sqrt{3},2)$;
設$\overrightarrow{n}=({x}_{2},{y}_{2},{z}_{2})$為平面ACG的一個法向量,
由$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AG}=0}\\{\overrightarrow{n}•\overrightarrow{CG}=0}\end{array}\right.$,可得$\left\{\begin{array}{l}{{x}_{2}+\sqrt{3}{y}_{2}=0}\\{2{x}_{2}+3{z}_{2}=0}\end{array}\right.$,取z2=-2,得$\overrightarrow{n}=(3,-\sqrt{3},-2)$.
∴cos<$\overrightarrow{m},\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}=\frac{1}{2}$.
∴二面角E-AG-C的大小為60°.
點評 本題考查空間角的求法,考查空間想象能力和思維能力,訓練了線面角的求法及利用空間向量求二面角的大小,是中檔題.


 同步學典一課多練系列答案
同步學典一課多練系列答案 經典密卷系列答案
經典密卷系列答案 金牌課堂練系列答案
金牌課堂練系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | p∧q | B. | p∧¬q | C. | ¬p∧q | D. | ¬p∧¬q |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (0,1]∪[2$\sqrt{3}$,+∞) | B. | (0,1]∪[3,+∞) | C. | (0,$\sqrt{2}$)∪[2$\sqrt{3}$,+∞) | D. | (0,$\sqrt{2}$]∪[3,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ω=$\frac{2}{3}$,φ=$\frac{π}{12}$ | B. | ω=$\frac{2}{3}$,φ=-$\frac{11π}{12}$ | C. | ω=$\frac{1}{3}$,φ=-$\frac{11π}{24}$ | D. | ω=$\frac{1}{3}$,φ=$\frac{7π}{24}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com