
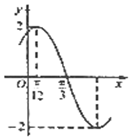
 已知函數$f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<\frac{π}{2})$的部分圖象如圖所示,下列說法正確的有( )個
已知函數$f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<\frac{π}{2})$的部分圖象如圖所示,下列說法正確的有( )個| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根據函數f(x)的部分圖象求出f(x)的解析式,再根據三角函數的圖象與性質,判斷題目中的命題是否正確.
解答 解:根據函數f(x)的部分圖象知,
A=2,$\frac{T}{4}$=$\frac{π}{3}$-$\frac{π}{12}$=$\frac{π}{4}$,
∴T=π,ω=$\frac{2π}{T}$=2;
由五點法畫圖知,x=$\frac{π}{12}$時f($\frac{π}{12}$)=2,
∴2×$\frac{π}{12}$+φ=$\frac{π}{2}$,解得φ=$\frac{π}{3}$;
∴f(x)=2sin(2x+$\frac{π}{3}$);
對于①,x=-$\frac{5π}{12}$f(-$\frac{5π}{12}$)=2sin(2×(-$\frac{5π}{12}$)+$\frac{π}{3}$)=-2
∴函數f(x)的圖象關于直線$x=-\frac{5π}{12}$對稱,命題正確;
對于②,x∈$[-\frac{π}{3},0]$時,2x+$\frac{π}{3}$∈[-$\frac{π}{3}$,$\frac{π}{3}$],f(x)是單調遞增函數,命題正確;
對于③,x=-$\frac{2π}{3}$f(-$\frac{2π}{3}$)=2sin[2×(-$\frac{2π}{3}$)+$\frac{π}{3}$]=0,
∴函數f(x)的圖象關于點$(-\frac{2π}{3},0)$對稱,命題正確;
對于④,將函數y=2sin2x的圖象向左平移$\frac{π}{3}$個單位,
得到y=2sin2(x+$\frac{π}{3}$)=2sin(2x+$\frac{2π}{3}$)的圖象,
不是f(x)的圖象,∴命題錯誤.
綜上,正確的命題序號是①②③,共3個.
故選:C.
點評 本題考查了三角函數的圖象與性質的應用問題,也考查了由函數的部分圖象求解析式的應用問題,是綜合題.


科目:高中數學 來源: 題型:選擇題
| A. | 160 | B. | 163 | C. | 166 | D. | 170 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | a<b<c | B. | b<a<c | C. | c<b<a | D. | c<a<b |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com