Question

10．已知實數x，y滿足：$\left\{\begin{array}{l}{2x+y-2≤0}\\{3x-2y+4≥0}\\{x-3y-1≤0}\end{array}\right.$，則3^x+9^y的最小值為（　　）

• A． 82
• B． 4
• C． $\frac{2}{9}$
• D． $\frac{2}{3}$

Answer 1

分析 由約束條件作出可行域，設z=2x+y，求出z的最大值，再利用基本不等式求解．

解答 解：由約束條件$\left\{\begin{array}{l}{2x+y-2≤0}\\{3x-2y+4≥0}\\{x-3y-1≤0}\end{array}\right.$作出可行域如圖，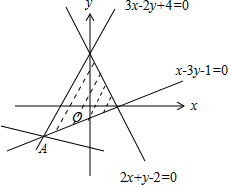

令z=x+2y，化為y=-$\frac{x}{2}+\frac{z}{2}$，
由圖可知，當直線y=-$\frac{x}{2}+\frac{z}{2}$過A（-2，-2）時直線y軸上的截距最小為z=-4，
∴3^x+9^y≥$2\sqrt{{3}^{x}•{3}^{2y}}=2\sqrt{{3}^{x+2y}}=2×\sqrt{{3}^{-4}}$=$\frac{2}{9}$．
故選：C．

點評 本題主要考查線性規劃的應用，利用目標函數的幾何意義以及指數函數的單調性的性質，結合數形結合的數學思想是解決此類問題的基本方法，是中檔題．