
分析 (Ⅰ)由橢圓定義得:|F2Q|=|F2P|+|PQ|=|F2P|+|PF1|=2a,點Q的軌跡是以F2為圓心,2a為半徑的圓,當QF2⊥F1F2時△QF1F2面積最大,推出ac=2,結合離心率,然后求解橢圓方程即可.
(Ⅱ)聯立$\left\{\begin{array}{l}y=kx+m\\ \frac{y^2}{4}+\frac{x^2}{3}=1\end{array}\right.$通過△=0,推出${k^2}=\frac{{{m^2}-4}}{3}$求出m≥2,設圓心F2(0,-1)到直線MN的距離為d,求出弦長,設點F1(0,1)到直線MN的距離為h,求出三角形的面積的表達式,然后求解范圍即可.
解答 解:(Ⅰ)由橢圓定義得:|F2Q|=|F2P|+|PQ|=|F2P|+|PF1|=2a,
所以點Q的軌跡是以F2為圓心,2a為半徑的圓.(1分)
當QF2⊥F1F2時△QF1F2面積最大,所以$\frac{1}{2}•2c•2a=4$得:ac=2(2分)
又$\frac{c}{a}=\frac{1}{2}$可得a=2,c=1. (3分)
所以Q點軌跡E的方程x2+(y+1)2=16,橢圓C的方程$\frac{y^2}{4}+\frac{x^2}{3}=1$(5分)
(Ⅱ)由$\left\{\begin{array}{l}y=kx+m\\ \frac{y^2}{4}+\frac{x^2}{3}=1\end{array}\right.$得(3k2+4)x2+6kmx+3m2-12=0△=36k2m2-4(3k2+4)(3m2-12)=0
化簡得:3k2-m2+4=0(7分)
所以,${k^2}=\frac{{{m^2}-4}}{3}$
由${k^2}=\frac{{{m^2}-4}}{3}≥0$及m>0得,m≥2
(8分)
設圓心F2(0,-1)到直線MN的距離為d,則$d=\frac{|m+1|}{{\sqrt{1+{k^2}}}}=\sqrt{\frac{3(m+1)}{m-1}}$
所以,弦長 $|MN|=2\sqrt{16-{d^2}}=2\sqrt{\frac{13m-19}{m-1}}$(9分)
設點F1(0,1)到直線MN的距離為h,則$h=\frac{|m-1|}{{\sqrt{1+{k^2}}}}=\sqrt{\frac{3(m-1)}{m+1}}$(10分)
所以,${S_{△{F_{\;}}_1MN}}=\frac{1}{2}|MN|•h=\sqrt{\frac{3(13m-19)}{m+1}}=\sqrt{39-\frac{96}{m+1}}$
由m≥2,得:$\sqrt{39-\frac{96}{m+1}}∈[\sqrt{7},\sqrt{39})$
所以,${S_{△{F_{\;}}_1MN}}$的取值范圍為$[\sqrt{7},\sqrt{39})$. (12分)
點評 本題考查橢圓方程的求法,直線與橢圓的位置關系的綜合應用,三角形的面積的求法,點到直線的距離公式的應用,考查轉化思想以及計算能力.


科目:高中數學 來源: 題型:選擇題
| A. | $2+\sqrt{3}$ | B. | $2-\sqrt{3}$ | C. | $2+\sqrt{5}$ | D. | $\sqrt{5}-2$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 160 | B. | 180 | C. | 200 | D. | 220 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | g(x)可能沒有零點 | B. | g(x)可能有1個零點 | C. | g(x)可能有2個零點 | D. | g(x)可能有3個零點 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
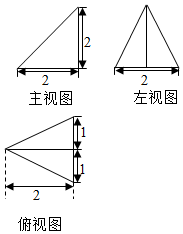 已知某個幾何體的三視圖如圖所示,根據圖中標出的尺寸,可得出這個幾何體的內切球半徑是( )
已知某個幾何體的三視圖如圖所示,根據圖中標出的尺寸,可得出這個幾何體的內切球半徑是( )| A. | $\frac{4}{3}$ | B. | $\frac{4}{9}$ | C. | $\sqrt{6}-2$ | D. | $3\sqrt{6}-6$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com