
分析 先由基本事件總數n=5,再由滿足雙曲線y=$\frac{7-3a}{x}$在第一、三象限且不等式組$\left\{\begin{array}{l}{2x+3>9}\\{x-a<0}\end{array}\right.$無解的a的個數m=3,由此能求出使雙曲線y=$\frac{7-3a}{x}$在第一、三象限且不等式組$\left\{\begin{array}{l}{2x+3>9}\\{x-a<0}\end{array}\right.$無解的概率.
解答 解:從-1,0,1,3,4,這五個數中任選一個數記為a,
基本事件總數n=5,
∵雙曲線y=$\frac{7-3a}{x}$在第一、三象限且不等式組$\left\{\begin{array}{l}{2x+3>9}\\{x-a<0}\end{array}\right.$無解,
∴$\left\{\begin{array}{l}{7-3a>0}\\{a<3}\end{array}\right.$,解得a$<\frac{7}{3}$,
∴滿足雙曲線y=$\frac{7-3a}{x}$在第一、三象限且不等式組$\left\{\begin{array}{l}{2x+3>9}\\{x-a<0}\end{array}\right.$無解的a的個數m=3,
∴使雙曲線y=$\frac{7-3a}{x}$在第一、三象限且不等式組$\left\{\begin{array}{l}{2x+3>9}\\{x-a<0}\end{array}\right.$無解的概率p=$\frac{m}{n}$=$\frac{3}{5}$.
故答案為:$\frac{3}{5}$.
點評 本題考查概率的求法,是基礎題,解題時要認真審題,注意等可能事件概率計算公式的合理運用.


科目:高中數學 來源: 題型:選擇題
| A. | 10 | B. | $10+2\sqrt{3}$ | C. | $10+2\sqrt{5}$ | D. | 12 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
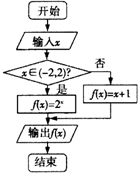
| A. | [0,log23] | B. | [-2,2] | C. | [0,log23]∪{2} | D. | [-2,log23]∪{2} |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | a>b>c | B. | c>a>b | C. | b>c>a | D. | c>b>a |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com