
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{\sqrt{30}}{5}$ | D. | $\frac{3\sqrt{5}}{5}$ |
分析 由等腰直角三角形的性質,求得A點坐標,代入雙曲線方程,求得a和b的關系,由離心率公式即可求得雙曲線的離心率.
解答 解:由題意可知:直線y=2b與y軸交于C點,△AOB為等腰直角三角形,
則∠BAO=∠ABO=45°,
則AC=2b,
△AOB為等腰直角三角形,A(-2b,2b),
將A代入雙曲線$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1,可得$\frac{{4b}^{2}}{{a}^{2}}-4=1$,∴b=$\frac{\sqrt{5}}{2}$a,
∴e=$\frac{c}{a}$=$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$=$\frac{3}{2}$,
雙曲線的離心率$\frac{3}{2}$,
故選:B.
點評 本題考查雙曲線的簡單的幾何性質,考查雙曲線的離心率公式,考查計算能力,屬于基礎題.


科目:高中數學 來源: 題型:選擇題
| A. | -$\frac{25}{4}$ | B. | $\frac{7}{4}$ | C. | -$\frac{9}{4}$ | D. | $\frac{41}{4}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
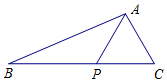 如圖,在△ABC中,點P在BC邊上,∠PAC=60°,PC=2,AP+AC=4.
如圖,在△ABC中,點P在BC邊上,∠PAC=60°,PC=2,AP+AC=4.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 8π | B. | 12π | C. | 20π | D. | 24π |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | l∥α | B. | l⊥α | C. | l?α | D. | A、C都有可能 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{9}{4}km$ | B. | $\frac{10}{4}km$ | C. | $\frac{11}{4}km$ | D. | $\frac{13}{4}km$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ①② | B. | ②③ | C. | ③④ | D. | ②④ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 30° | B. | 30°或150° | C. | 60° | D. | 60°或120° |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com