
| A. | 若?服從正態分布N(1,2),且P(?>2)=0.1,則P(0<?<2)=0.2 | |
| B. | 命題:“?x>1,x2>1”的否定是“?x≤1,x2≤1” | |
| C. | 直線ax+y+2=0與ax-y+4=0垂直的充要條件為a=±1 | |
| D. | “若xy=0,則x=0或y=0”的逆否命題為“若x≠0或y≠0,則xy≠0” |
分析 A,?服從正態分布N(1,2),其正態曲線關于直線x=1對稱,由P(?>2)=0.1得P(0<?<2)=0.8,;
B,命題:“?x>1,x2>1”的否定是“?x>1,x2≤1”,只否定結論;
C,直線ax+y+2=0與ax-y+4=0垂直時⇒a•a+1×(-1)=0⇒a=±1,把a=±1代入直線方程驗證垂直;
D,”或的否定是“且“.
解答 解:對于A,?服從正態分布N(1,2),其正態曲線關于直線x=1對稱,由P(?>2)=0.1得P(0<?<2)=0.8,故錯;
對于B,命題:“?x>1,x2>1”的否定是“?x>1,x2≤1”,只否定結論,故錯;
對于C,直線ax+y+2=0與ax-y+4=0垂直時⇒a•a+1×(-1)=0⇒a=±1,把a=±1代入直線方程驗證垂直,故正確;
對于D,“若xy=0,則x=0或y=0”的逆否命題為“若x≠0且y≠0,則xy≠0“,”或的否定是“且“,故錯.
故選:C.
點評 本題考查了命題真假判定,涉及到了大量的基礎知識,屬于基礎題.


科目:高中數學 來源: 題型:選擇題
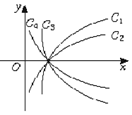 圖中曲線是對數函數y=logax的圖象,已知a取$\sqrt{3}$,$\frac{4}{3}$,$\frac{3}{5}$,$\frac{1}{10}$四個值,則相應于C1,C2,C3,C4的a值依次為( )
圖中曲線是對數函數y=logax的圖象,已知a取$\sqrt{3}$,$\frac{4}{3}$,$\frac{3}{5}$,$\frac{1}{10}$四個值,則相應于C1,C2,C3,C4的a值依次為( )| A. | $\frac{4}{3}$,$\sqrt{3}$,$\frac{3}{5}$,$\frac{1}{10}$ | B. | $\sqrt{3}$,$\frac{4}{3}$,$\frac{1}{10}$,$\frac{3}{5}$ | C. | $\sqrt{3}$,$\frac{4}{3}$,$\frac{3}{5}$,$\frac{1}{10}$ | D. | $\frac{4}{3}$,$\sqrt{3}$,$\frac{1}{10}$,$\frac{3}{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{{{e^2}+1}}{2}$ | B. | $\frac{{{e^2}-3}}{2}$ | C. | $\frac{{{e^2}+3}}{2}$ | D. | $\frac{{{e^2}-5}}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{3}{2}$ | B. | $\frac{4}{9}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 大前提錯誤 | B. | 小前提錯誤 | ||
| C. | 推理形式錯誤 | D. | 大前提、小前提及推理形式都錯誤 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com