
分析 由已知得x>0,y>0,x+y=4,由基本不等式,得xy≤$(\frac{x+y}{2})^{2}$=4,由此能示出三棱錐O-ABC的體積的最大值.
解答 解:∵三棱錐O-ABC中,OA=x,OB=y,x+y=4,
∴x>0,y>0,x+y=4,
由基本不等式,得:
xy≤$(\frac{x+y}{2})^{2}$=4,
∵OA,OB,OC兩兩互相垂直,OC=1,
∴三棱錐O-ABC的體積V=$\frac{1}{3}×\frac{1}{2}×OA×OB×OC=\frac{1}{6}xy≤\frac{2}{3}$,
三棱錐O-ABC的體積的最大值為$\frac{2}{3}$.
故答案為:$\frac{2}{3}$.
點評 本題考查三棱錐的體積的最大值的求法,是基礎題,解題時要認真審題,注意空間思維能力的培養.


科目:高中數學 來源: 題型:選擇題
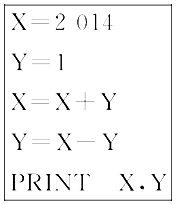
| A. | 2 015,2 013 | B. | 2 013,2 015 | C. | 2 015,2 015 | D. | 2 015,2 014 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | $\frac{6}{5}$ | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [0,$\frac{1}{5})$ | B. | ($\frac{1}{5},\frac{1}{4}$) | C. | ($\frac{1}{5},\frac{1}{3}$) | D. | [l,3] |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | p∧q | B. | (¬p)∧(¬q) | C. | p∧(¬q) | D. | (¬p)∧q |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
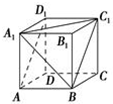 如圖在正方體ABCDA1B1C1D1中判斷下列位置關系:
如圖在正方體ABCDA1B1C1D1中判斷下列位置關系:查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com