
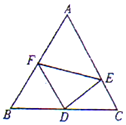
 如圖,在邊長為2的正三角形△ABC中,D為BC的中點,E,F分別在邊CA,AB上.
如圖,在邊長為2的正三角形△ABC中,D為BC的中點,E,F分別在邊CA,AB上.分析 (1)在△CDE中,由已知及余弦定理可得CE2-CE-1=0,進而解得CE的值.
(2)設∠CDE=α,300≤α≤900,在△CDE中,由正弦定理,可求DE=$\frac{\sqrt{3}}{2sin(60°+α)}$,$DF=\frac{{\sqrt{3}}}{2sinα}$,利用三角形面積公式可求S△DEF=$\frac{3\sqrt{3}}{4+8sin(2α-30°)}$,由范圍300≤2α-300≤1500,利用正弦函數的圖象和性質即可得解.
解答 解:(1)在△CDE中,$∠DCE={60^0},CD=1,DE=\sqrt{2}$,
由余弦定理得,DE2=CD2+CE2-2×CD×CE×cos60°,
得CE2-CE-1=0,解得$CE=\frac{{\sqrt{5}+1}}{2}$;
(2)設∠CDE=α,300≤α≤900,
在△CDE中,由正弦定理,得$\frac{DE}{sin∠DCE}=\frac{DC}{sin∠CED}$,
所以$DE=\frac{{sin{{60}^0}}}{{sin({{{60}^0}+α})}}=\frac{{\sqrt{3}}}{{2sin({{{60}^0}+α})}}$,同理$DF=\frac{{\sqrt{3}}}{2sinα}$,
故${S_{△DEF}}=\frac{1}{2}×DE×DF×sin∠EDF=\frac{{3\sqrt{3}}}{{16sinαsin({{{60}^0}+α})}}=\frac{{3\sqrt{3}}}{{4+8sin({2α-{{30}^0}})}}$,
因為300≤α≤900,300≤2α-300≤1500,
所以當α=600時,sin(2α-300)的最大值為1,此時△DEF的面積取到最小值.
即∠CDE=60°時,△DEF的面積的最小值為$\frac{{\sqrt{3}}}{4}$.
點評 此題考查了正弦、余弦定理,三角形的面積公式,以及同角三角函數間的基本關系,正弦函數的圖象和性質的綜合應用,熟練掌握定理及公式是解本題的關鍵,屬于中檔題.


 百年學典課時學練測系列答案
百年學典課時學練測系列答案 仁愛英語同步練習冊系列答案
仁愛英語同步練習冊系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $({-∞,-\frac{3}{2}})$ | B. | $({-∞,-\frac{3}{2}}]∪({\frac{{3\sqrt{3}}}{8},\frac{3}{2}}]$ | C. | $({-∞,-\frac{3}{2}})∪({\frac{{3\sqrt{3}}}{8},\frac{3}{2}})$ | D. | $[{-\frac{3}{2},+∞})$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {0,1,2} | B. | [0,2] | C. | {0,2} | D. | (0,2) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com