
分析 (1)根據an=Sn-Sn-1得出遞推公式,得出{an}為等比數列,再計算a1,得出通項公式;
(2)計算bn,利用裂項法求和,根據求和公式列方程得出n.
解答 解:(1)由an=2-2Sn得2Sn=2-an,
∴2Sn-1=2-an-1,(n≥2)
當n=1時,a1=$\frac{2}{3}$,
當n≥2時,2an=an-1-an,即an=$\frac{1}{3}$an-1,
∴{an}是以$\frac{2}{3}$為首項,以$\frac{1}{3}$為公比的等比數列,
∴an=$\frac{2}{3}$×($\frac{1}{3}$)n-1=$\frac{2}{{3}^{n}}$.
(2)Sn=$\frac{\frac{2}{3}(1-\frac{1}{{3}^{n}})}{1-\frac{1}{3}}$=1-$\frac{1}{{3}^{n}}$,∴bn=log3$\frac{1}{{3}^{n}}$=-n,∴$\frac{1}{{b}_{n}{b}_{n+1}}$=$\frac{1}{n(n+1)}$=$\frac{1}{n}-\frac{1}{n+1}$,
∴$\frac{1}{{b}_{2}{b}_{3}}$+$\frac{1}{{b}_{3}{b}_{4}}$+…+$\frac{1}{{b}_{n}{b}_{n+1}}$=$\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}$+…+$\frac{1}{n}-\frac{1}{n+1}$=$\frac{1}{2}-$$\frac{1}{n+1}$,
∴$\frac{1}{2}-$$\frac{1}{n+1}$=$\frac{25}{51}$,解得n=101.
點評 本題考查了等比數列的判斷,裂項法求和,屬于基礎題.


科目:高中數學 來源: 題型:解答題
| 分數 | [0,90) | [90,105) | [105,1200) | [120,135) | [135,150) |
| 甲班頻數 | 5 | 6 | 4 | 4 | 1 |
| 乙班頻數 | 1 | 3 | 6 | 5 |
| 甲班 | 乙班 | 總計 | |
| 成績優良 | |||
| 成績不優良 | |||
| 總計 |
| P(K2≥k0) | 0.10 | 0.050 | 0.025 | 0.010 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $2\sqrt{3}$ | B. | 4 | C. | $4\sqrt{3}$ | D. | 8 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,在四棱錐P-ABCD中,已知PA⊥平面ABCD,四邊形ABCD是梯形,∠ABC=90°,BC∥AD,且$PA=AB=BC=\frac{1}{2}AD=1$.
如圖,在四棱錐P-ABCD中,已知PA⊥平面ABCD,四邊形ABCD是梯形,∠ABC=90°,BC∥AD,且$PA=AB=BC=\frac{1}{2}AD=1$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 若α∩β=a,β∩γ=b,a∥b,則α∥γ | B. | 若a∥α,a∥β,b∥α,b∥β,則α∥β | ||
| C. | 若α⊥β,α∩β=a,b?β,a⊥b,則b⊥α | D. | 若a?α,b?α,l⊥α,l⊥b,則l⊥α |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
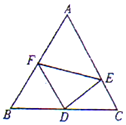 如圖,在邊長為2的正三角形△ABC中,D為BC的中點,E,F分別在邊CA,AB上.
如圖,在邊長為2的正三角形△ABC中,D為BC的中點,E,F分別在邊CA,AB上.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com