Question

15．函數$y=2\sqrt{2}sin（ωx+φ）$（其中ω＞0，0＜φ＜π）的圖象的一部分如圖所示，則（　　）

• A． $ω=\frac{π}{8}{，_{\;}}φ=\frac{3π}{4}$
• B． $ω=\frac{π}{8}{，_{\;}}φ=\frac{π}{4}$
• C． $ω=\frac{π}{4}{，_{\;}}φ=\frac{π}{2}$
• D． $ω=\frac{π}{4}{，_{\;}}φ=\frac{3π}{4}$

Answer 1

分析 先利用圖象中求得函數的周期，求得ω，最后根據x=2時取最大值，求得φ，即可得解．

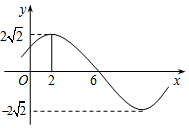
解答 解：如圖根據函數的圖象可得：函數的周期為（6-2）×4=16，
又∵ω＞0，
∴ω=$\frac{2π}{T}$=$\frac{π}{8}$，
當x=2時取最大值，即2$\sqrt{2}$sin（2×$\frac{π}{8}$+φ）=2$\sqrt{2}$，可得：2×$\frac{π}{8}$+φ=2kπ+$\frac{π}{2}$，k∈Z，
∴φ=2kπ+$\frac{π}{4}$，k∈Z，
∵0＜φ＜π，
∴φ=$\frac{π}{4}$，
故選：B．

點評 本題主要考查了由y=Asin（ωx+φ）的部分圖象確定其解析式，考查了學生基礎知識的運用和圖象觀察能力，屬于基本知識的考查．