
| A. | p∧q | B. | (¬p)∨q | C. | (¬p)∧q | D. | p∧(¬q) |
分析 命題p:?x∈(-∞,0),$(\frac{2}{3})^{x}$>1,即2x>3x,可得p是真命題.命題q:x∈(0,$\frac{π}{2}$),令f(x)=x-sinx,利用導數研究其單調性即可得出真假.
解答 解:命題p:?x∈(-∞,0),$(\frac{2}{3})^{x}$>1,即2x>3x,因此p是真命題.
命題q:x∈(0,$\frac{π}{2}$),令f(x)=x-sinx,f′(x)=1-cosx>0,因此函數f(x)在x∈(0,$\frac{π}{2}$)單調遞增,∴f(x)>f(0)=0.∴?x∈(0,$\frac{π}{2}$),sinx<x,因此q是假命題.
則下列命題為真命題的是p∧(¬q).
故選:D.
點評 本題考查了指數函數的單調性、利用導數研究函數的單調性、簡易邏輯的判定方法,考查了推理能力與計算能力,屬于中檔題.


 新卷王期末沖刺100分系列答案
新卷王期末沖刺100分系列答案 全能闖關100分系列答案
全能闖關100分系列答案科目:高中數學 來源: 題型:選擇題

| A. | $\frac{9}{2}$π+24 | B. | $\frac{9}{2}$π+30 | C. | 9π+54 | D. | 36π+30 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (x-$\frac{3}{2}$)2+y2=25 | B. | (x+$\frac{3}{2}$)2+y2=$\frac{1}{4}$ | C. | (x-$\frac{3}{2}$)2+y2=$\frac{25}{4}$ | D. | x2+(y-$\frac{3}{2}$)2=$\frac{5}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
 如圖,三棱柱ABC-A1B1C1中,側棱AA1⊥底面A1B1C1,AA1=AC=BC=1,∠ACB=90°,D是A1B1的中點,F是BB1上的點,AB1,DF交于點E,且AB1⊥DF,則下列結論中不正確的是( )
如圖,三棱柱ABC-A1B1C1中,側棱AA1⊥底面A1B1C1,AA1=AC=BC=1,∠ACB=90°,D是A1B1的中點,F是BB1上的點,AB1,DF交于點E,且AB1⊥DF,則下列結論中不正確的是( )| A. | CE與BC1異面且垂直 | B. | AB1⊥C1F | ||
| C. | △C1DF是直角三角形 | D. | DF的長為$\frac{{\sqrt{6}}}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{2}{5}$ | B. | -$\frac{2}{5}$ | C. | $\frac{2}{3}$ | D. | -$\frac{2}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
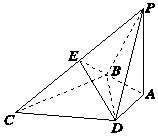 如圖所示,PA與四邊形ABCD所在平面垂直,且PA=BC=CD=BD,AB=AD,PD⊥DC.
如圖所示,PA與四邊形ABCD所在平面垂直,且PA=BC=CD=BD,AB=AD,PD⊥DC.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $-\frac{4}{3}$ | D. | -3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com