Question

9．設正四面體ABCD的四個面BCD，ACD，ABD，ABC的中心，分別為O₁，O₂，O₃，O₄則直線O₁O₂與O₃O₄所成角的大小為$\frac{π}{2}$．

Answer 1

分析 以O₁為原點，O₁C為x軸，O₁A為z軸，建立空間直角坐標系，利用向量法能求出O₁O₂與O₃O₄所成的角．

解答 解：以O₁為原點，O₁C為x軸，O₁A為z軸，建立空間直角坐標系，建立如圖所求空間直角坐標系，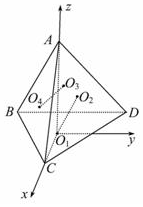
設AB=1，則B（-$\frac{\sqrt{3}}{6}$，-$\frac{1}{2}$，0），D（-$\frac{\sqrt{3}}{6}$，$\frac{1}{2}$，0），C（$\frac{\sqrt{3}}{3}$，0，0），A（0，0，$\frac{\sqrt{6}}{3}$），
∴O₁（0，0，0），${O}_{2}（\frac{\sqrt{3}}{18}，\frac{1}{6}，\frac{\sqrt{6}}{9}）$，${O}_{3}（-\frac{\sqrt{3}}{9}，0，\frac{\sqrt{6}}{9}）$，${O}_{4}（\frac{\sqrt{3}}{18}，-\frac{1}{6}，\frac{\sqrt{6}}{9}）$，
$\overrightarrow{{O}_{1}{O}_{2}}$=（$\frac{\sqrt{3}}{18}，\frac{1}{6}，\frac{\sqrt{6}}{9}$），$\overrightarrow{{O}_{3}{O}_{4}}$=（$\frac{\sqrt{3}}{6}，-\frac{1}{6}，0$），
∴$\overrightarrow{{O}_{1}{O}_{2}}$$\overrightarrow{{O}_{3}{O}_{4}}$=$\frac{3}{108}-\frac{1}{36}+0=0$，
∴O₁O₂⊥O₃O₄，
∴直線O₁O₂與O₃O₄所成角的大小為$\frac{π}{2}$．
故答案為：$\frac{π}{2}$．

點評 本題考查兩異面直線所成角的大小的求法，是基礎題，解題時要認真審題，注意向量法的合理運用．