
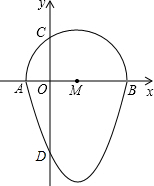
 如圖,我們把一個半圓與拋物線的一部分圍成的封閉圖形稱為“果圓”,已知點A、B、C、D分別是“果圓”與坐標軸的交點,AB為半圓的直徑,拋物線的解析式為y=x2-2x-3,求這個“果圓”被y軸截得線段CD的長3+$\sqrt{3}$.
如圖,我們把一個半圓與拋物線的一部分圍成的封閉圖形稱為“果圓”,已知點A、B、C、D分別是“果圓”與坐標軸的交點,AB為半圓的直徑,拋物線的解析式為y=x2-2x-3,求這個“果圓”被y軸截得線段CD的長3+$\sqrt{3}$. 分析 將x=0代入拋物線的解析式得y=-3,故此可得到DO的長,然后令y=0可求得點A和點B的坐標,故此可得到AB的長,由M為圓心可得到MC和OM的長,然后依據勾股定理可求得OC的長,最后依據CD=OC+OD求解即可.
解答 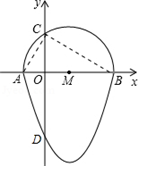 解:連接AC,BC.
解:連接AC,BC.
∵拋物線的解析式為y=x2-2x-3,
∴點D的坐標為(0,-3),
∴OD的長為3.
設y=0,則0=x2-2x-3,解得:x=-1或3,
∴A(-1,0),B(3,0).
∴AO=1,BO=3,AB=4,M(1,0).
∴MC=2,OM=1.
在Rt△COB中,OC=$\sqrt{C{M}^{2}-O{M}^{2}}$=$\sqrt{3}$.
∴CD=CO+OD=3+$\sqrt{3}$,即這個“果圓”被y軸截得的線段CD的長3+$\sqrt{3}$.
故答案為:3+$\sqrt{3}$.
點評 本題主要考查的是二次函數的綜合應用,解答本題主要應用了坐標軸上點的坐標特點,圓的概念和性質,勾股定理等知識點,求的點D的坐標以及OC的長是解題的關鍵.


科目:初中數學 來源: 題型:解答題
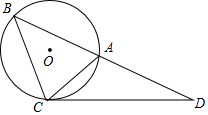 如圖所示,△ABC的外接圓⊙O的半徑為2,過點C作∠ACD=∠ABC,交BA的延長線于點D,若∠ABC=45°,∠D=30°.
如圖所示,△ABC的外接圓⊙O的半徑為2,過點C作∠ACD=∠ABC,交BA的延長線于點D,若∠ABC=45°,∠D=30°.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
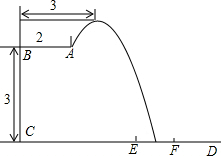 2016年里約奧運會,中國跳水隊贏得8個項目中的7塊金牌,優秀成績的取得離不開艱辛的訓練.某跳水運動員在進行跳水訓練時,身體(看成一點)在空中的運動路線是如圖所示的一條拋物線,已知跳板AB長為2米,跳板距水面CD的高BC為3米,訓練時跳水曲線在離起跳點水平距離1米時達到距水面最大高度k米,現以CD為橫軸,CB為縱軸建立直角坐標系.
2016年里約奧運會,中國跳水隊贏得8個項目中的7塊金牌,優秀成績的取得離不開艱辛的訓練.某跳水運動員在進行跳水訓練時,身體(看成一點)在空中的運動路線是如圖所示的一條拋物線,已知跳板AB長為2米,跳板距水面CD的高BC為3米,訓練時跳水曲線在離起跳點水平距離1米時達到距水面最大高度k米,現以CD為橫軸,CB為縱軸建立直角坐標系.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
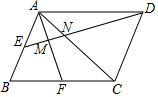 如圖,點E,F分別是?ABCD兩邊AB、BC的中點,且AF、AC分別與ED交于M、N兩點,有下列結論:①MN:ME=2:3;②MN:DN=1:4;③N是DE的三等分點;④△AMN~△DMA.其中正確的是:①③.(把所有正確結論的序號都選上)
如圖,點E,F分別是?ABCD兩邊AB、BC的中點,且AF、AC分別與ED交于M、N兩點,有下列結論:①MN:ME=2:3;②MN:DN=1:4;③N是DE的三等分點;④△AMN~△DMA.其中正確的是:①③.(把所有正確結論的序號都選上)查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\sqrt{12}$-$\sqrt{3}$=$\sqrt{3}$ | B. | (-3)2=6 | C. | 3a4-2a2=a2 | D. | (-a3)2=a5 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | m=1 | B. | m=0 | C. | m=-1 | D. | m=2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com