
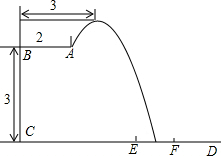
 2016年里約奧運會,中國跳水隊贏得8個項目中的7塊金牌,優秀成績的取得離不開艱辛的訓練.某跳水運動員在進行跳水訓練時,身體(看成一點)在空中的運動路線是如圖所示的一條拋物線,已知跳板AB長為2米,跳板距水面CD的高BC為3米,訓練時跳水曲線在離起跳點水平距離1米時達到距水面最大高度k米,現以CD為橫軸,CB為縱軸建立直角坐標系.
2016年里約奧運會,中國跳水隊贏得8個項目中的7塊金牌,優秀成績的取得離不開艱辛的訓練.某跳水運動員在進行跳水訓練時,身體(看成一點)在空中的運動路線是如圖所示的一條拋物線,已知跳板AB長為2米,跳板距水面CD的高BC為3米,訓練時跳水曲線在離起跳點水平距離1米時達到距水面最大高度k米,現以CD為橫軸,CB為縱軸建立直角坐標系.分析 (1)根據拋物線頂點坐標M(3,4),可設拋物線解析為:y=a(x-3)2+4,將點A(2,3)代入可得;
(2)在(1)中函數解析式中令y=0,求出x即可;
(3)若跳水運動員在區域EF內(含點E,F)入水達到訓練要求,則在函數y=a(x-3)2+k中當x=$\frac{19}{4}$米,y>0,當x=$\frac{21}{4}$米時y<0,解不等式即可得.
解答 解:(1)如圖所示: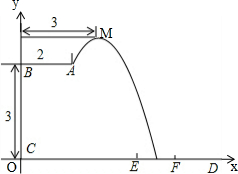
根據題意,可得拋物線頂點坐標M(3,4),A(2,3)
設拋物線解析為:y=a(x-3)2+4,
則3=a(2-3)2+4,
解得:a=-1,
故拋物線解析式為:y=-(x-3)2+4;
(2)由題意可得:當y=0,則0=-(x-3)2+4,
解得:x1=1,x2=5,
故拋物線與x軸交點為:(5,0),
當k=4時,求運動員落水點與點C的距離為5米;
(3)根據題意,拋物線解析式為:y=a(x-3)2+k,
將點A(2,3)代入可得:a+k=3,即a=3-k
若跳水運動員在區域EF內(含點E,F)入水,
則當x=$\frac{19}{4}$時,y=$\frac{49}{16}$a+k≥0,即$\frac{49}{16}$(3-k)+k≥0,
解得:k≤$\frac{49}{11}$,
當x=$\frac{21}{4}$時,y=$\frac{81}{16}$a+k≤0,即$\frac{81}{16}$(3-k)+k≤0,
解得:k≥$\frac{243}{65}$,
故$\frac{243}{65}$≤k≤$\frac{49}{11}$.
點評 此題主要考查了二次函數的應用,根據題意利用頂點式求出二次函數解析式是解題基礎,判斷入水的位置對應的拋物線上點的坐標特點是解題關鍵.


科目:初中數學 來源: 題型:解答題
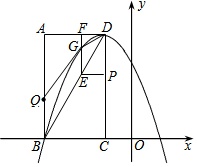 如圖,在平面直角坐標系中,已知矩形ABCD的三個頂點A(-3,4)、B(-3,0)、C(-1,0).以D為頂點的拋物線y=ax2+bx+c過點B.動點P從點D出發,沿DC邊向點C運動,同時動點Q從點B出發,沿BA邊向點A運動,點P、Q運動的速度均為每秒1個單位,運動的時間為t秒.過點P作PE⊥CD交BD于點E,過點E作EF⊥AD于點F,交拋物線于點G.
如圖,在平面直角坐標系中,已知矩形ABCD的三個頂點A(-3,4)、B(-3,0)、C(-1,0).以D為頂點的拋物線y=ax2+bx+c過點B.動點P從點D出發,沿DC邊向點C運動,同時動點Q從點B出發,沿BA邊向點A運動,點P、Q運動的速度均為每秒1個單位,運動的時間為t秒.過點P作PE⊥CD交BD于點E,過點E作EF⊥AD于點F,交拋物線于點G.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
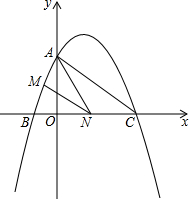 如圖,已知二次函數y=ax2+$\frac{3}{2}$x+c的圖象與y軸交于點A(0,4),與x軸交于點B,C,點C的坐標為(8,0),連接AC、AC.
如圖,已知二次函數y=ax2+$\frac{3}{2}$x+c的圖象與y軸交于點A(0,4),與x軸交于點B,C,點C的坐標為(8,0),連接AC、AC.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
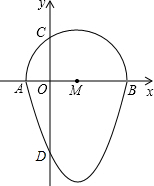 如圖,我們把一個半圓與拋物線的一部分圍成的封閉圖形稱為“果圓”,已知點A、B、C、D分別是“果圓”與坐標軸的交點,AB為半圓的直徑,拋物線的解析式為y=x2-2x-3,求這個“果圓”被y軸截得線段CD的長3+$\sqrt{3}$.
如圖,我們把一個半圓與拋物線的一部分圍成的封閉圖形稱為“果圓”,已知點A、B、C、D分別是“果圓”與坐標軸的交點,AB為半圓的直徑,拋物線的解析式為y=x2-2x-3,求這個“果圓”被y軸截得線段CD的長3+$\sqrt{3}$.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 7 | B. | 8 | C. | 4+2$\sqrt{3}$ | D. | 4+$\sqrt{3}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com