
| A. | 7 | B. | 8 | C. | 4+2$\sqrt{3}$ | D. | 4+$\sqrt{3}$ |
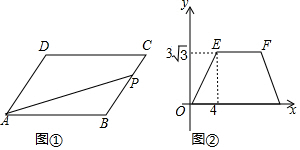
分析 作CM⊥AB于M,根據三角形面積公式可得當點P在CD上運動時,△PAB的面積不變,再聯系函數圖象可得BC=cm,則AB=3cm,然后根據三角函數求出CM,三角形面積公式求出AB,即可得出結果.
解答 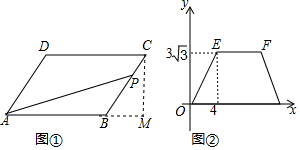 解:作CM⊥AB于M如圖所示:
解:作CM⊥AB于M如圖所示:
當點P在CD上運動時,△PAB的面積不變,
由圖②得:BC=4cm,
∵∠ABC=120°,
∴∠CBM=60°,
∴CM=BC•sin60°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
∵△ABC的面積=$\frac{1}{2}$AB•CM=$\frac{1}{2}$AB×2$\sqrt{3}$=3$\sqrt{3}$,
∴AB=3cm,
∴點F的橫坐標為4+3=7.
故選:A.
點評 本題考查了平行四邊形的性質、動點問題的函數圖象.解決本題的關鍵是利用函數圖象和三角形面積確定AB的長.


科目:初中數學 來源: 題型:解答題
 如圖,矩形ABCD中,E是邊BC的一點,F是邊CD的中點,CE=k•BE,且四邊形AECF的面積為2.
如圖,矩形ABCD中,E是邊BC的一點,F是邊CD的中點,CE=k•BE,且四邊形AECF的面積為2.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
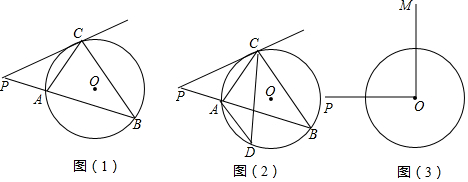
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
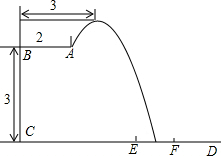 2016年里約奧運會,中國跳水隊贏得8個項目中的7塊金牌,優秀成績的取得離不開艱辛的訓練.某跳水運動員在進行跳水訓練時,身體(看成一點)在空中的運動路線是如圖所示的一條拋物線,已知跳板AB長為2米,跳板距水面CD的高BC為3米,訓練時跳水曲線在離起跳點水平距離1米時達到距水面最大高度k米,現以CD為橫軸,CB為縱軸建立直角坐標系.
2016年里約奧運會,中國跳水隊贏得8個項目中的7塊金牌,優秀成績的取得離不開艱辛的訓練.某跳水運動員在進行跳水訓練時,身體(看成一點)在空中的運動路線是如圖所示的一條拋物線,已知跳板AB長為2米,跳板距水面CD的高BC為3米,訓練時跳水曲線在離起跳點水平距離1米時達到距水面最大高度k米,現以CD為橫軸,CB為縱軸建立直角坐標系.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com